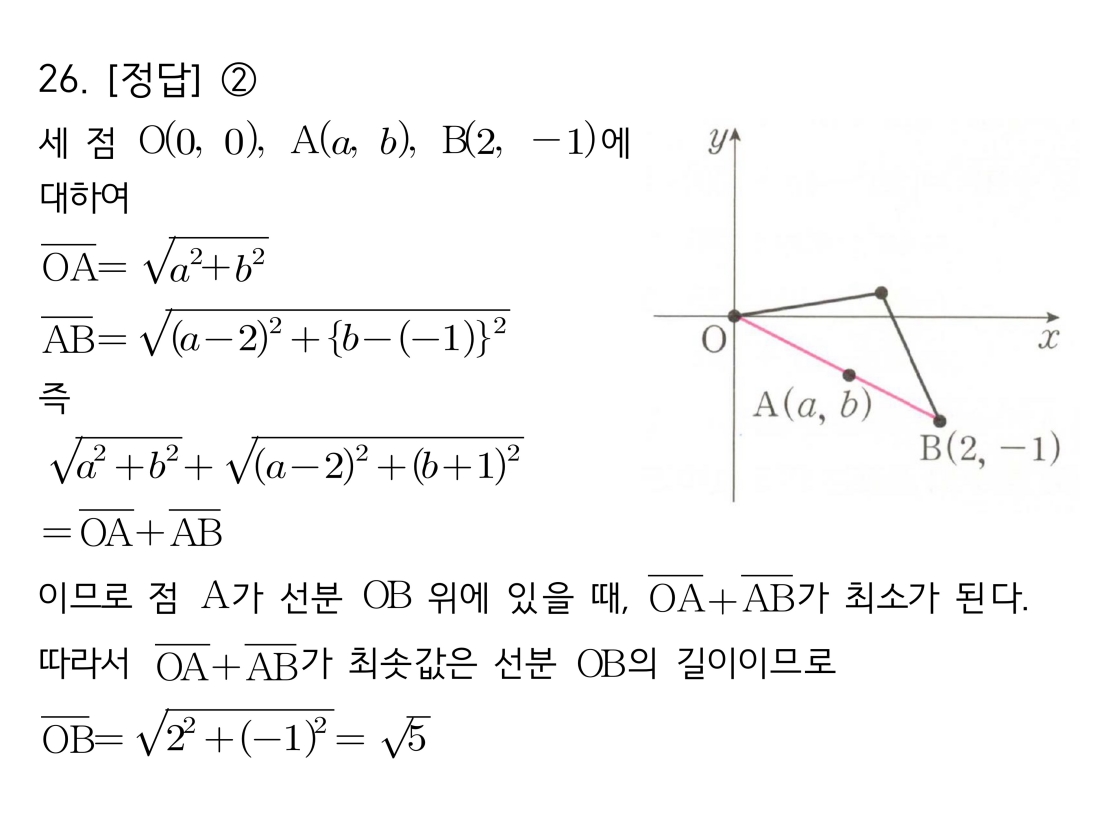
“ [문제 25] 핵심 개념 및 풀이 전략 두 정점과 임의의 한 점을 잇는 두 선분의 길이 합(AP+PB)의 최솟값을 묻는 가장 기본적인 유형입니다. 접근법:1. 삼각형의 결정 조건에 의해, 점 P가 어디에 있든 항상 **AP + PB ≥ AB** 가 성립합니다.2. 등호는 점 P가 **선분 AB 위에 있을 때** 성립하므로, AP+PB의 최솟값은 바로 선분 AB의 길이 … 더 읽기
“ [문제 26] 핵심 개념 및 풀이 전략 25번 문제와 완전히 동일한 원리를 적용하는 문제입니다. 점의 좌표만 바뀌었습니다. 접근법:1. [cite_start]문제의 식은 원점 O(0,0)과 점 A(a,b) 사이의 거리, 그리고 점 A(a,b)와 점 B(2,-1) 사이의 거리의 합을 의미합니다. [cite: 1170-1174]2. 이 거리의 합(OA+AB)이 최소가 되려면, 세 점 O, A, B가 **일직선 위에 있어야** 하며, 점 A는 선분 … 더 읽기
“ [문제 27] 핵심 개념 및 풀이 전략 네 점까지의 거리의 합(PO+PA+PB+PC)의 최솟값을 묻는 응용 문제입니다. 접근법:1. 거리의 합을 두 쌍으로 묶어서 생각합니다: (PA+PC) + (PO+PB).2. 삼각형의 결정 조건에 의해 PA+PC의 최솟값은 **선분 AC의 길이**이고, PO+PB의 최솟값은 **선분 OB의 길이**입니다.3. 전체 합이 최소가 되는 경우는 점 P가 **두 대각선(AC와 OB)의 교점**에 위치할 때입니다.4. 따라서 최솟값은 … 더 읽기
“ [문제 28] 핵심 개념 및 풀이 전략 두 선분의 길이의 차(|PB-PA|)의 최댓값을 구하는 문제입니다. 합의 최솟값 문제와 원리를 비교하며 이해해야 합니다. 접근법:1. 삼각형의 결정 조건에 의해, 점 P가 어디에 있든 항상 **|PB-PA| ≤ AB** 가 성립합니다.2. 등호는 세 점 P, A, B가 **일직선 위에 있을 때** 성립합니다.3. 따라서 길이의 차의 최댓값은 바로 **선분 AB의 … 더 읽기
“ [문제 29] 핵심 개념 및 풀이 전략 움직이는 두 물체 사이의 최단 거리를 묻는 실생활 활용 문제입니다. 시간에 따른 위치를 좌표로 설정하는 것이 핵심입니다. 접근법:1. 교차로 O를 원점(0,0)으로 설정합니다.2. [cite_start]출발 후 t시간이 지났을 때의 두 학생 A, B의 위치를 각각 t에 대한 좌표로 표현합니다. [cite: 1193]3. 두 학생 사이의 거리를 t에 대한 식으로 나타내면, … 더 읽기
“ [문제 30] 핵심 개념 및 풀이 전략 선분 길이의 ‘제곱의 합’의 최솟값을 구하는 문제입니다. 거리의 합 최솟값 문제와는 풀이법이 완전히 다릅니다. 접근법:1. x축 위의 점 P의 좌표를 (b, 0)으로 설정합니다.2. AP²과 BP²을 각각 b에 대한 식으로 나타냅니다. 제곱이므로 루트가 사라져 계산이 간편합니다.3. 두 식을 더하면 b에 대한 간단한 **이차함수**가 만들어집니다.4. 이 이차함수의 꼭짓점을 찾아 … 더 읽기
“ [문제 31] 핵심 개념 및 풀이 전략 30번 문제에서 점 P의 위치가 ‘x축 위’가 아닌 임의의 점으로 확장된 유형입니다. 접근법:1. 임의의 점 P의 좌표를 (a, b)로 설정합니다.2. AP² + BP²의 값을 a와 b에 대한 식으로 나타냅니다.3. 식을 a에 대한 완전제곱식과 b에 대한 완전제곱식으로 각각 정리합니다.4. 식이 최소가 되려면 각각의 완전제곱식이 0이 되어야 하므로, 이를 … 더 읽기
“ [문제 32] 핵심 개념 및 풀이 전략 거리의 제곱의 합 최솟값 문제에서 점 P가 특정 직선 위에 있도록 조건이 추가된 유형입니다. 접근법:1. 점 P가 직선 y=x+3 위에 있으므로, 좌표를 (a, a+3)으로 설정하여 미지수를 하나로 줄입니다.2. AP² + BP²의 값을 a에 대한 식으로 나타내고 전개합니다.3. 결과적으로 a에 대한 이차함수가 만들어지며, 이 함수의 꼭짓점에서 최솟값이 발생합니다.4. … 더 읽기
“ [문제 33] 핵심 개념 및 풀이 전략 삼각형의 중선과 세 변의 길이 사이에 성립하는 관계식인 파푸스의 중선정리를 증명하는 과정입니다. 접근법:1. 증명을 위해 도형을 좌표평면 위에 편리하게 배치하는 것이 중요합니다. 변 BC의 중점 M을 **원점(0,0)**에, 변 BC를 x축 위에 놓습니다.2. 이렇게 하면 각 꼭짓점의 좌표를 간단한 문자로 표현할 수 있습니다. (예: B(-c,0), C(c,0), A(a,b))3. 중선정리 … 더 읽기
“ [문제 34] 핵심 개념 및 풀이 전략 삼각형의 세 변의 길이가 주어졌을 때 중선의 길이를 구하는 문제로, 파푸스의 중선정리를 직접적으로 활용합니다. 접근법:1. 삼각형 ABC에서 변 BC의 중점이 M일 때, 중선정리 공식 **AB² + AC² = 2(AM² + BM²)** 이 성립합니다.2. 문제에 주어진 세 변의 길이를 공식에 그대로 대입합니다.3. [cite_start]변 BC의 길이가 10이므로, 변 BM의 … 더 읽기
마플시너지 공통수학2 문제 전체보기 링크 바로가기