쎈 공통수학1 · 4단원 이차방정식
520번 · \(f(\alpha)=f(\beta)=-1\) → \(f(x)+1=0\)의 근이 \(\alpha, \beta\)
— \(f(x)+1=(x-\alpha)(x-\beta)=x^2-3x-5\) 직접 이용!
난이도 : 중
📹 풀이 영상
📋 이 포스팅에서 확인할 수 있어요
- 📹 풀이 영상 (f(α)=k 조건 처리 전략)
- 🖼️ 교재 해설 이미지
- 🔑 f(α)=−1 → f(α)+1=0 → f(x)+1=0의 두 근이 α, β
- 📐 f(x)+1=(x−α)(x−β)=x²−3x−5 → f(x)=x²−3x−6 → f(3)=−6
- ⚠️ f(x)+1의 두 근이 α, β임을 이용해 원래 방정식(α, β의 방정식)과 연결!
- ⏱️ 내신 / 수능 목표 풀이 시간
📌 문제 핵심 파악
이차방정식 \(x^2-3x-5=0\)의 두 근을 \(\alpha\), \(\beta\)라 할 때,
이차식 \(f(x)\)가 \(f(\alpha)=f(\beta)=-1\)을 만족시키고 \(x^2\)의 계수가 1일 때,
\(f(3)\)의 값을 구하는 문제입니다.
🔑 핵심 아이디어
\(f(\alpha)=-1\)이면 \(f(\alpha)+1=0\)
마찬가지로 \(f(\beta)+1=0\)
→ \(f(x)+1=0\)의 두 근이 \(\alpha\), \(\beta\)!
→ \(f(x)+1=(x-\alpha)(x-\beta)\) (\(x^2\) 계수가 1이므로)
\(f(\alpha)=-1\)이면 \(f(\alpha)+1=0\)
마찬가지로 \(f(\beta)+1=0\)
→ \(f(x)+1=0\)의 두 근이 \(\alpha\), \(\beta\)!
→ \(f(x)+1=(x-\alpha)(x-\beta)\) (\(x^2\) 계수가 1이므로)
✏️ 단계별 풀이
1
f(x)+1 결정
\(f(x)+1 = (x-\alpha)(x-\beta)\)
\(\alpha\), \(\beta\)가 \(x^2-3x-5=0\)의 두 근이므로:
\[(x-\alpha)(x-\beta) = x^2-3x-5\] 따라서 \(f(x)+1 = x^2-3x-5\)
\(f(x)+1 = (x-\alpha)(x-\beta)\)
\(\alpha\), \(\beta\)가 \(x^2-3x-5=0\)의 두 근이므로:
\[(x-\alpha)(x-\beta) = x^2-3x-5\] 따라서 \(f(x)+1 = x^2-3x-5\)
2
f(x) 결정
\[f(x) = x^2-3x-5-1 = x^2-3x-6\]
\[f(x) = x^2-3x-5-1 = x^2-3x-6\]
3
f(3) 계산
\[f(3) = 9-9-6 = -6\]
\[f(3) = 9-9-6 = -6\]
정답 : ② \(f(3)=-6\)
🧠 외워두면 좋은 패턴
\(f(\alpha)=f(\beta)=k\) 유형 완전 루틴
① \(f(\alpha)=k\) → \(f(\alpha)-k=0\)
② \(f(x)-k=0\)의 두 근이 \(\alpha\), \(\beta\) → \(f(x)-k=(x-\alpha)(x-\beta)\)
③ \((x-\alpha)(x-\beta)\)는 \(\alpha\), \(\beta\)의 방정식에서 직접 읽어옴
④ \(f(x) = (x-\alpha)(x-\beta)+k\)
① \(f(\alpha)=k\) → \(f(\alpha)-k=0\)
② \(f(x)-k=0\)의 두 근이 \(\alpha\), \(\beta\) → \(f(x)-k=(x-\alpha)(x-\beta)\)
③ \((x-\alpha)(x-\beta)\)는 \(\alpha\), \(\beta\)의 방정식에서 직접 읽어옴
④ \(f(x) = (x-\alpha)(x-\beta)+k\)
⚠️ 이런 실수 조심!
- f(x)=x²−3x−5라고 쓰는 실수 — f(x)+1=x²−3x−5이므로 f(x)=x²−3x−6!
- f(x)−k에서 k=−1이면 f(x)+1=0이 되는 변환 확인
⏱️ 목표 풀이 시간
내신 시험
3분
수능·모의고사
2분
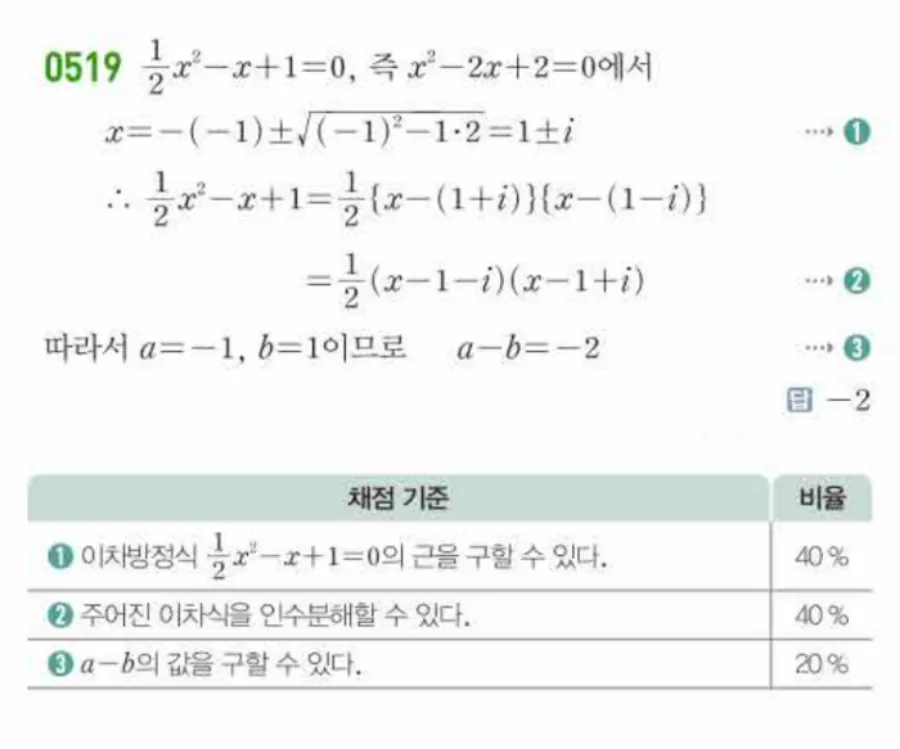
🖼️ 교재 해설 이미지