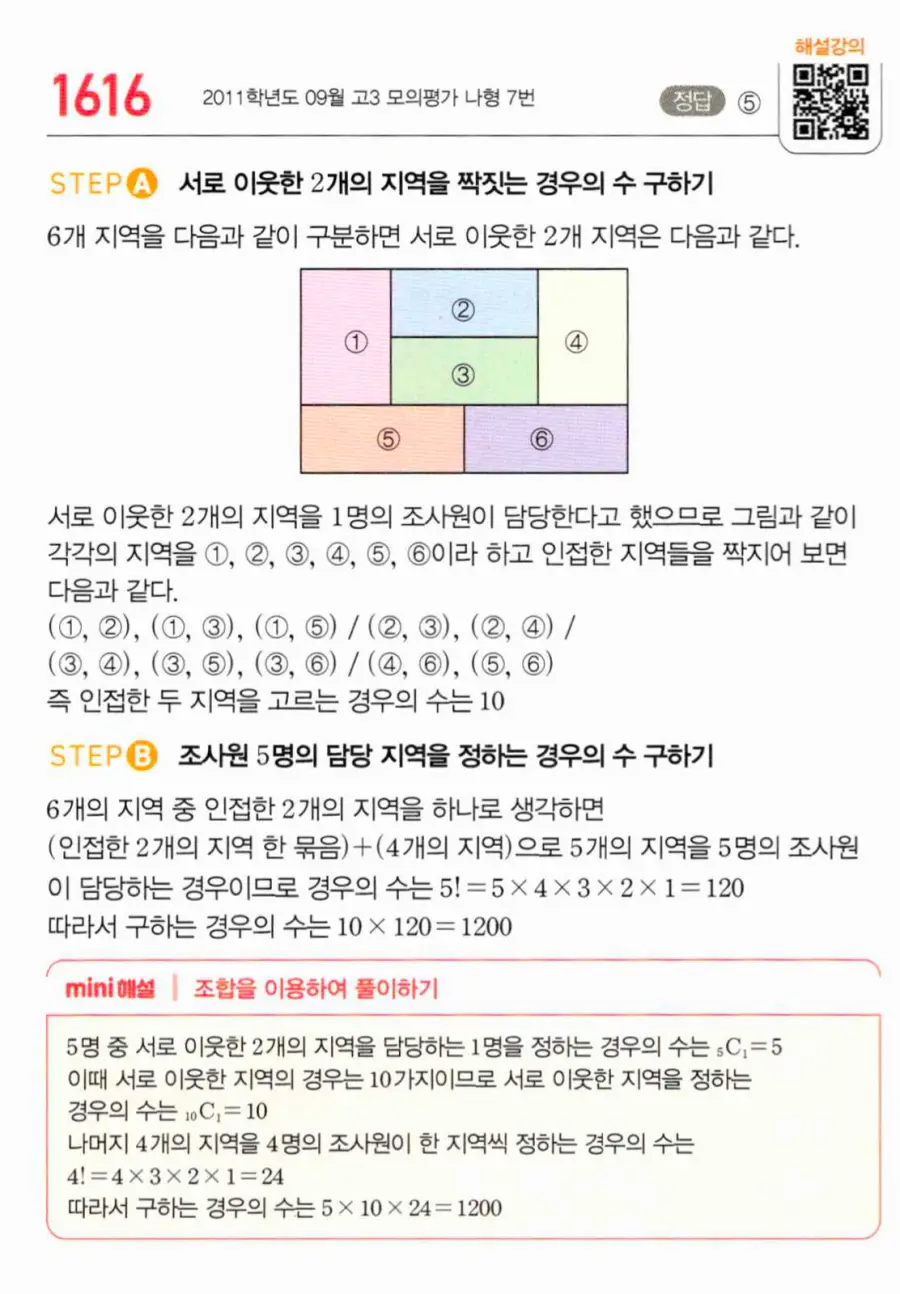
TOUGH
마플시너지 공통수학1 12단원 1623번 – 이차방정식의 근과 계수의 관계를 활용한 순열·조합 문제
📌 문제 요약
이차방정식의 두 근이 주어졌을 때, 근과 계수의 관계를 이용하여 ₙCᵣ과 ₙPᵣ의 값을 구하고, 이를 통해 자연수 n, r의 값을 결정하는 문제입니다. 정답은 n + r = 7입니다.
🔑 핵심 단서
- 이차방정식의 근과 계수의 관계로 두 근의 합과 두 근의 곱을 세운다.
- ₙCᵣ = ₙPᵣ / r! 관계를 활용하여 r!의 값을 먼저 결정한다.
- ₙPᵣ 값을 확정한 뒤 n(n−1) = 20 이차방정식을 풀어 n ≥ 2 조건을 확인한다.
💡 왜 이렇게 풀어야 할까?
이 문제의 핵심은 이차방정식의 계수 속에 ₙCᵣ과 ₙPᵣ이 숨어 있다는 점입니다. 근과 계수의 관계를 세우면 두 식이 연립되고, ₙCᵣ = ₙPᵣ / r! 공식으로 연결하면 r!을 특정할 수 있습니다. r이 정해지면 ₙPᵣ로부터 n에 대한 이차방정식이 나오므로, 자연수 조건을 만족하는 해를 선택하면 됩니다.
🎬 해설 영상
⚠️ 자주 하는 실수
- 근과 계수의 관계에서 부호 실수 — 두 근의 합은 −(일차항계수)/(이차항계수)임을 놓치기 쉽습니다.
- ₙCᵣ = ₙPᵣ / r! 관계를 거꾸로 적용하거나, r! 계산 오류를 범하는 경우가 많습니다.
- n에 대한 이차방정식에서 음수 해를 걸러내지 않고 답으로 적는 실수에 주의하세요.
📚 개념·연산 포스팅 추천
고등수학 개념사전 049 │ 근과 계수의 관계 고등수학 개념사전 229 │ 순열 기초 고등수학 개념사전 230 │ ₙPᵣ 계산 고등수학 개념사전 231 │ 조합 기초 연산 워크시트 29 │ 이차방정식의 근과 계수의 관계 연산 워크시트 60 │ 순열 연산 워크시트 62 │ 조합
마플시너지공통수학11623번TOUGH근과계수의관계순열조합nCrnPr이차방정식경우의수조합과순열관계고등수학문제풀이12단원순열조합연결r팩토리얼자연수조건수능대비내신대비고1수학