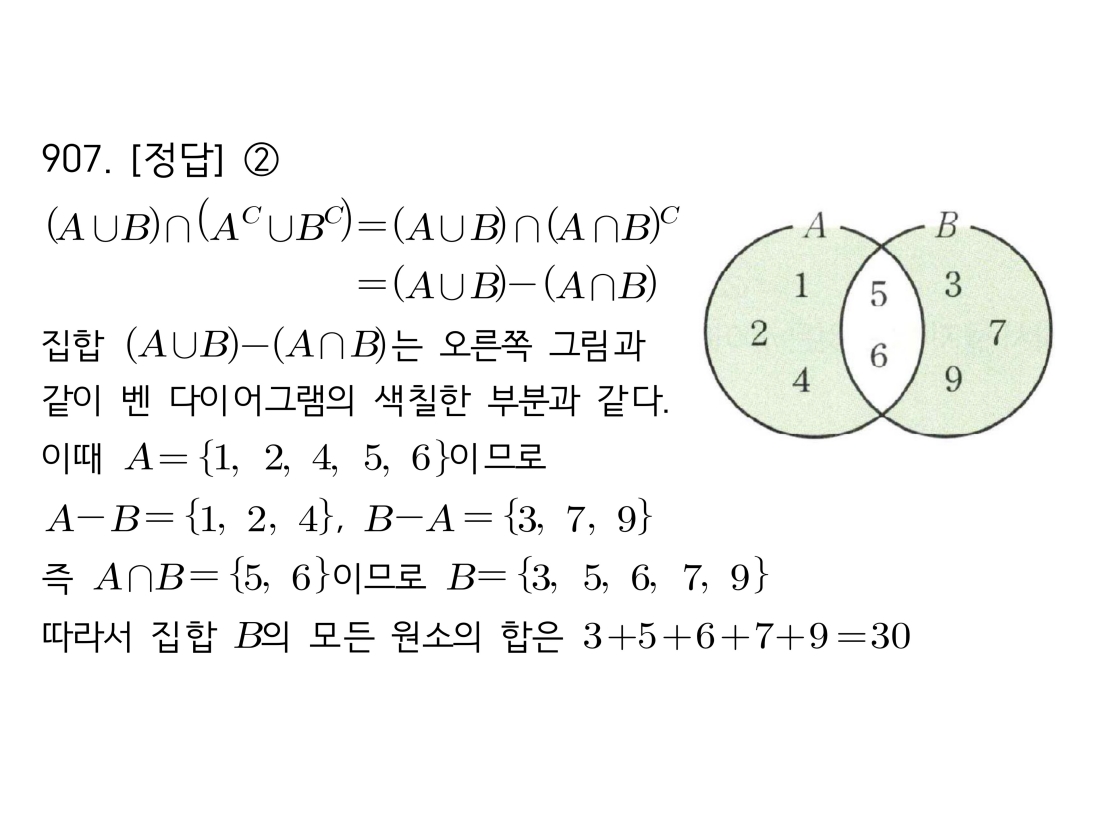
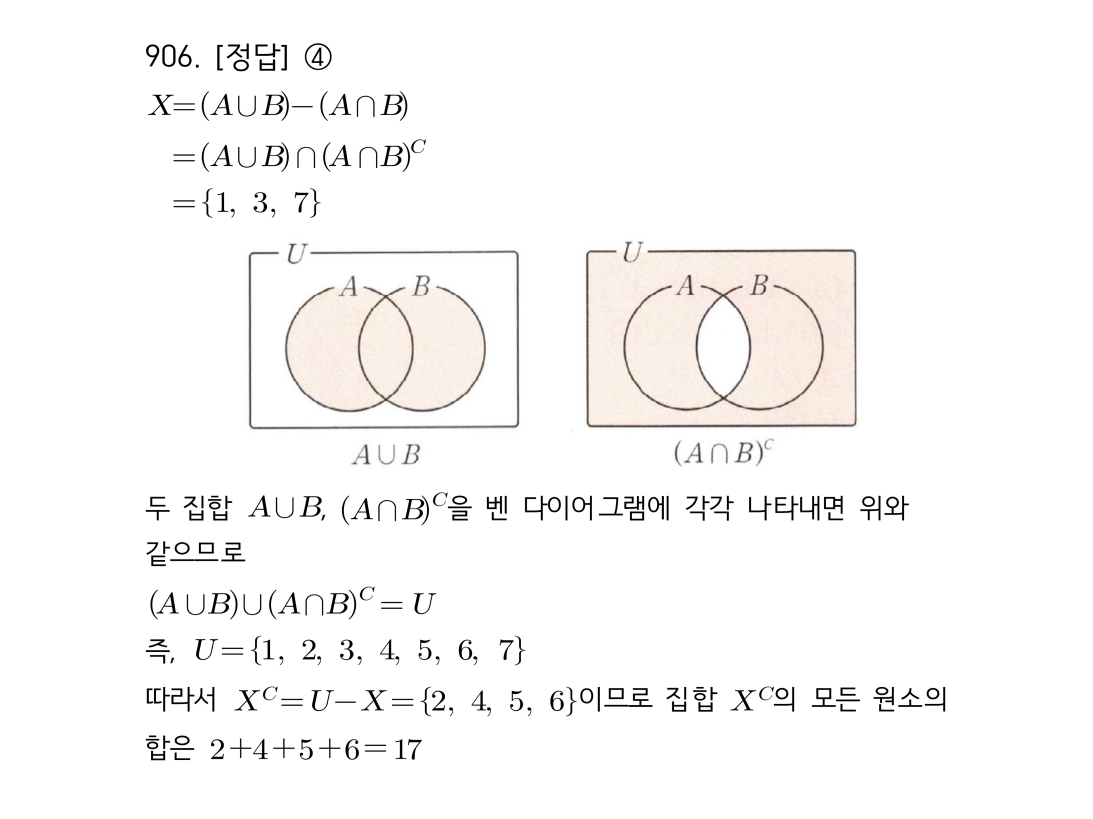
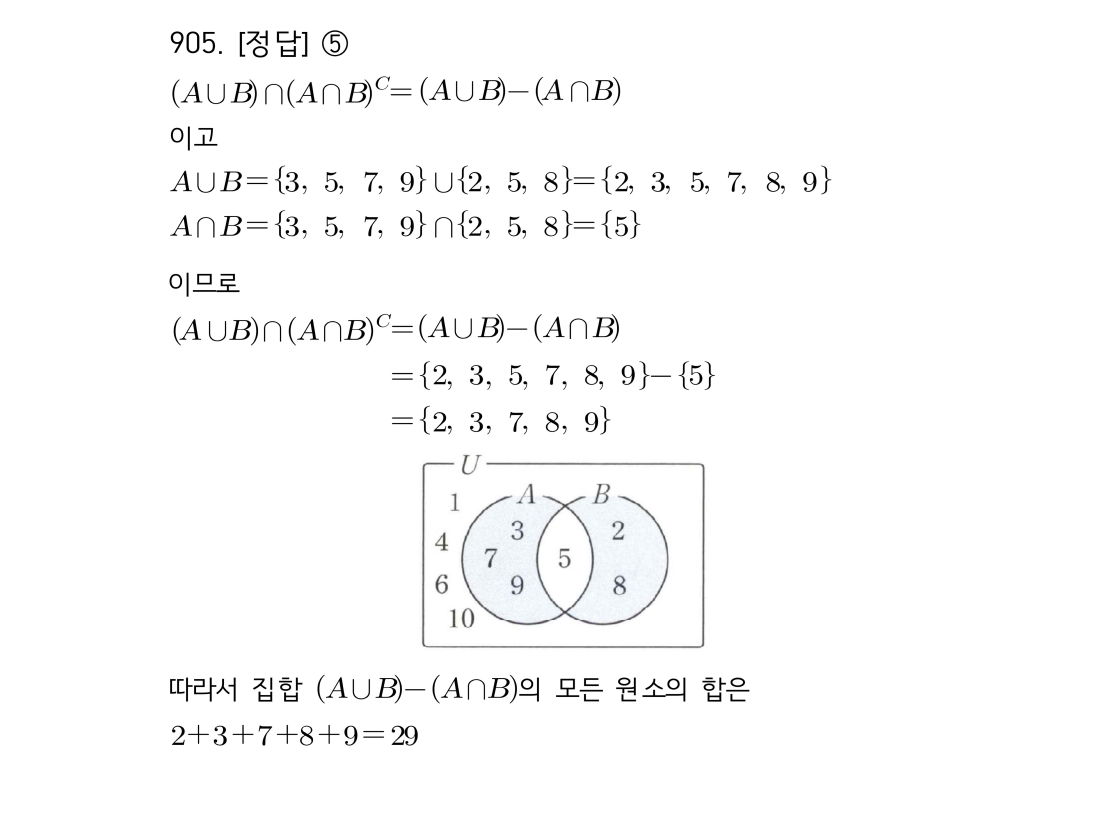
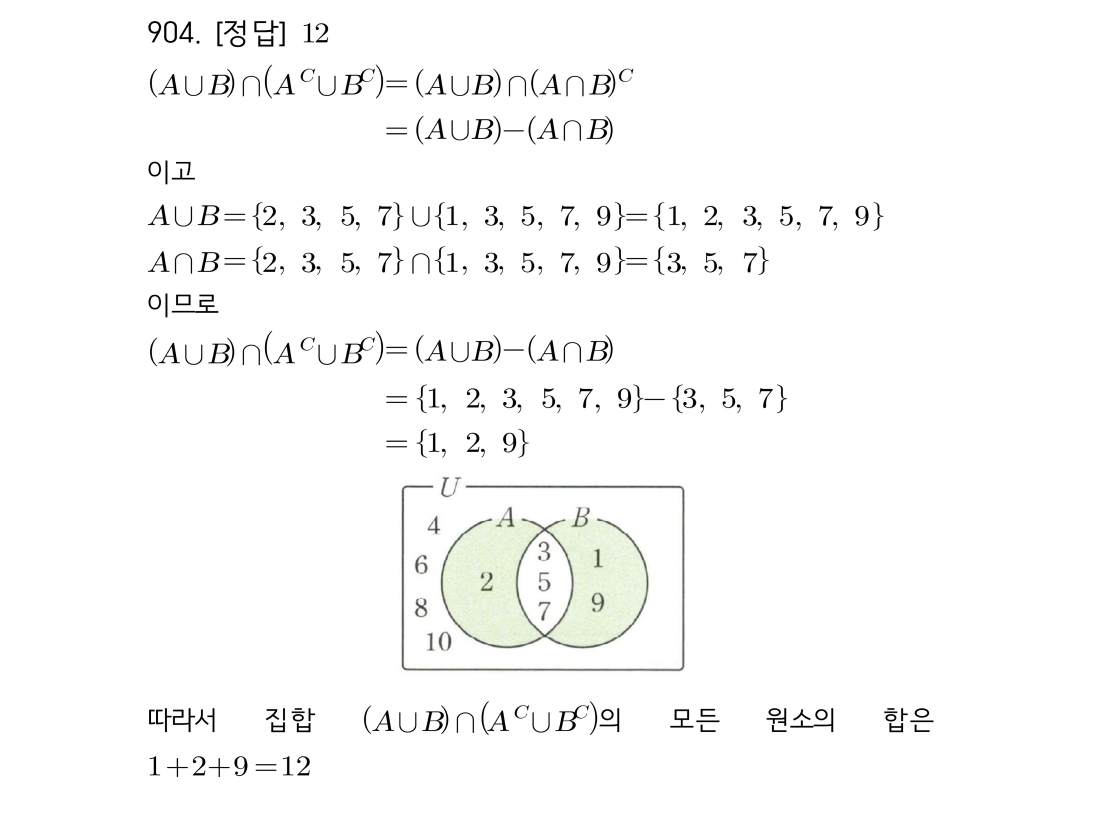
마플시너지공통수학2풀이해설0910고퀄리티 풀이영상제공0910 진리집합 포함 관계를 이용한 미지수 범위 찾기
“ [문제 910] 핵심 개념 및 풀이 전략 909번 문제와 동일하게, 명제가 참이 되도록 진리집합의 포함 관계를 이용하는 문제입니다. 접근법:1. 명제 p→q가 참이므로, 진리집합 P⊂Q 여야 합니다.2. P = {x | a-3 < x < a+1}, Q = {x | 1 ≤ x ≤ 7}3. 수직선 위에 P가 Q에 포함되도록 그림을 그립니다.4. P의 시작점과 끝점이 ... 더 읽기