[영상 있음] 쎈대수 0108번 – 거듭제곱근의 곱이 -9일 때 k 구하기 (평가원 기출)

📝 오늘의 문제 (쎈대수 0108번)

함수 \(f(x) = -(x-2)^2 + k\)에 대하여 다음 조건을 만족시키는 자연수 \(n\)의 개수가 2일 때, 상수 \(k\)의 값은?

① 8       ② 9       ③ 10       ④ 11       ⑤ 12

• ✅ 짝수제곱근 중 실수: 양수 \(A\)의 네제곱근 중 실수는 \(\pm \sqrt[4]{A}\)이며, 그 곱은 항상 \(-(\sqrt[4]{A})^2\)입니다.
• ✅ 지수의 성질: \(\sqrt{3^{f(n)}} = 3^{\frac{f(n)}{2}}\)
• ✅ 이차함수의 대칭성: \(f(x) = a(x-p)^2 + q\)는 \(x=p\)를 축으로 대칭을 이룹니다.

Step 1. \(f(n)\)의 조건 도출하기

주어진 수 \(\sqrt{3^{f(n)}} = 3^{\frac{f(n)}{2}}\)의 네제곱근 중 실수인 것은 다음과 같습니다.
\(\pm \sqrt[4]{3^{\frac{f(n)}{2}}} = \pm 3^{\frac{f(n)}{8}}\)
이 두 실수의 곱이 \(-9\)이므로:
\(3^{\frac{f(n)}{8}} \times \left( -3^{\frac{f(n)}{8}} \right) = -3^{\frac{f(n)}{4}} = -3^2\)
따라서 지수를 비교하면 \(\frac{f(n)}{4} = 2\)가 되어, \(f(n) = 8\)을 만족해야 합니다.

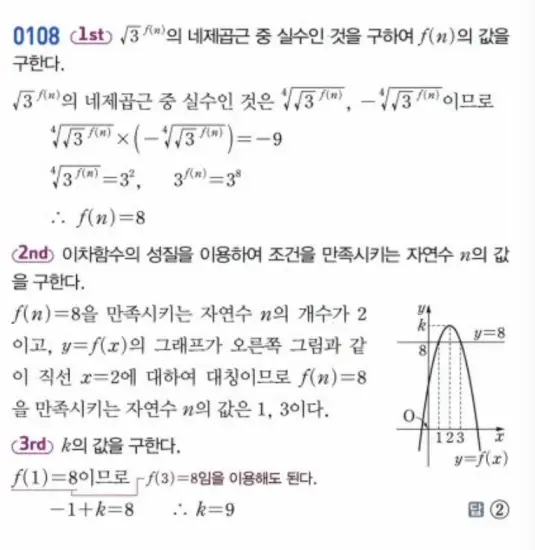
Step 2. 대칭성을 이용한 자연수 \(n\) 찾기

함수 \(f(x) = -(x-2)^2 + k\)는 직선 \(x=2\)에 대하여 대칭인 위로 볼록한 포물선입니다.
방정식 \(f(n) = 8\)을 만족하는 자연수 \(n\)이 정확히 2개가 존재해야 하므로, 그 자연수들은 축인 \(x=2\)에서 좌우로 같은 거리만큼 떨어져 있어야 합니다.
자연수 중에서 이 조건을 만족하는 가장 작은 조합은 \(n=1\)과 \(n=3\)입니다. (축 2에서 거리가 1로 동일)

Step 3. 상수 \(k\) 값 결정

\(f(1) = 8\) (또는 \(f(3) = 8\))이 성립해야 하므로 식에 대입하면:
\(-(1-2)^2 + k = 8\)
\(-1 + k = 8\)
따라서 \(k = 9\)가 도출됩니다. (정답 ②번)

🔥 1등급 꿀팁 & 실수 포인트

[실수 포인트]

• “실수인 것을 모두 곱한 값”이라는 표현에서 실수 근이 2개 존재함을 인지해야 합니다. 만약 근이 하나였다면 곱이 음수가 나올 수 없습니다.

[쌤의 꿀팁]

• 이차함수 문제에서 자연수의 개수 조건이 나오면 90% 이상 ‘축의 대칭성’을 묻는 문제입니다. 계산으로 \(n\)을 풀려고 하기보다 그래프를 그려서 대칭인 자연수 쌍을 먼저 찾으세요!