마플시너지 공통수학1 1-2 항등식과 나머지정리 (2) 답지
안녕하세요. **마플시너지 공통수학1** **1-2 항등식과 나머지정리** 두 번째 파트(2/3) 정답 및 해설입니다.
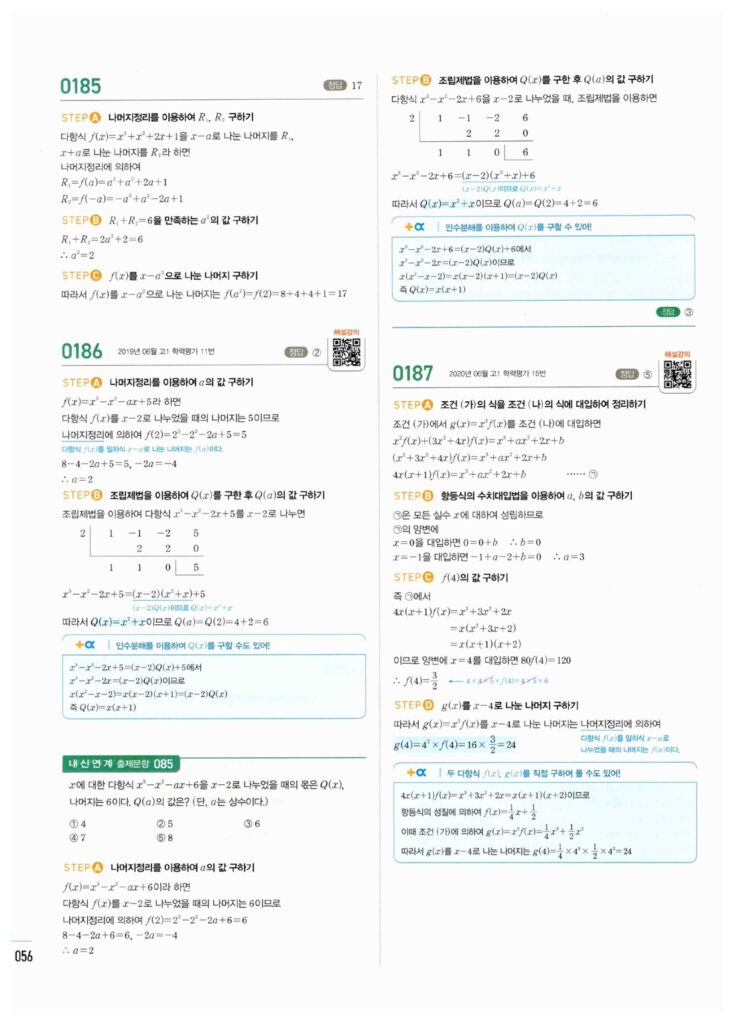
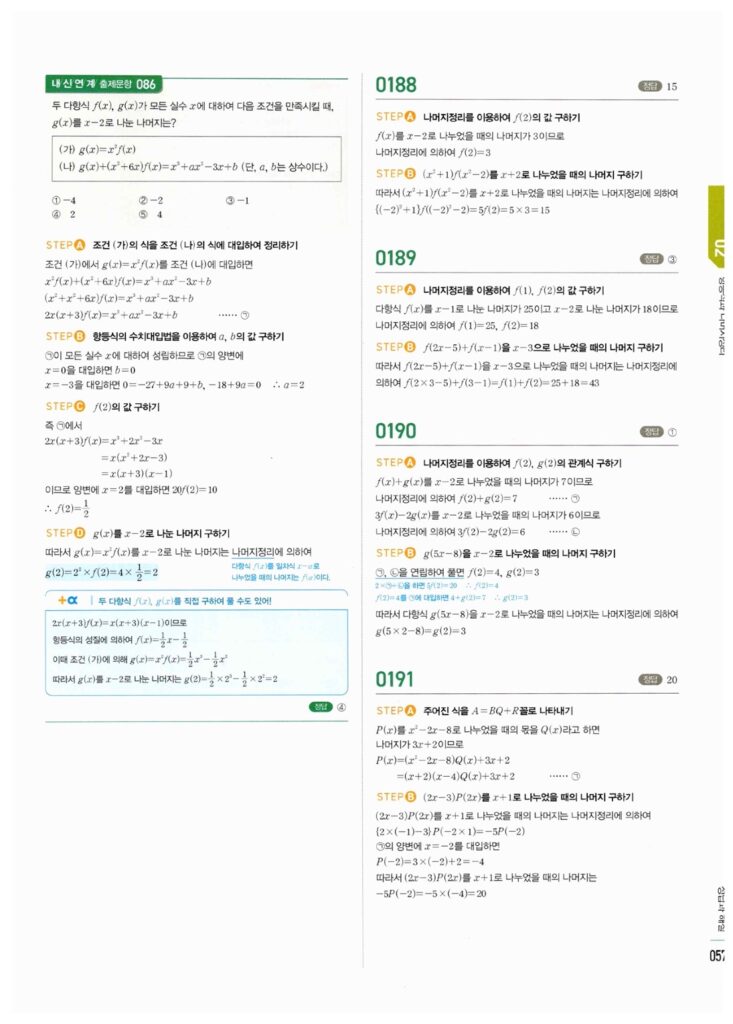
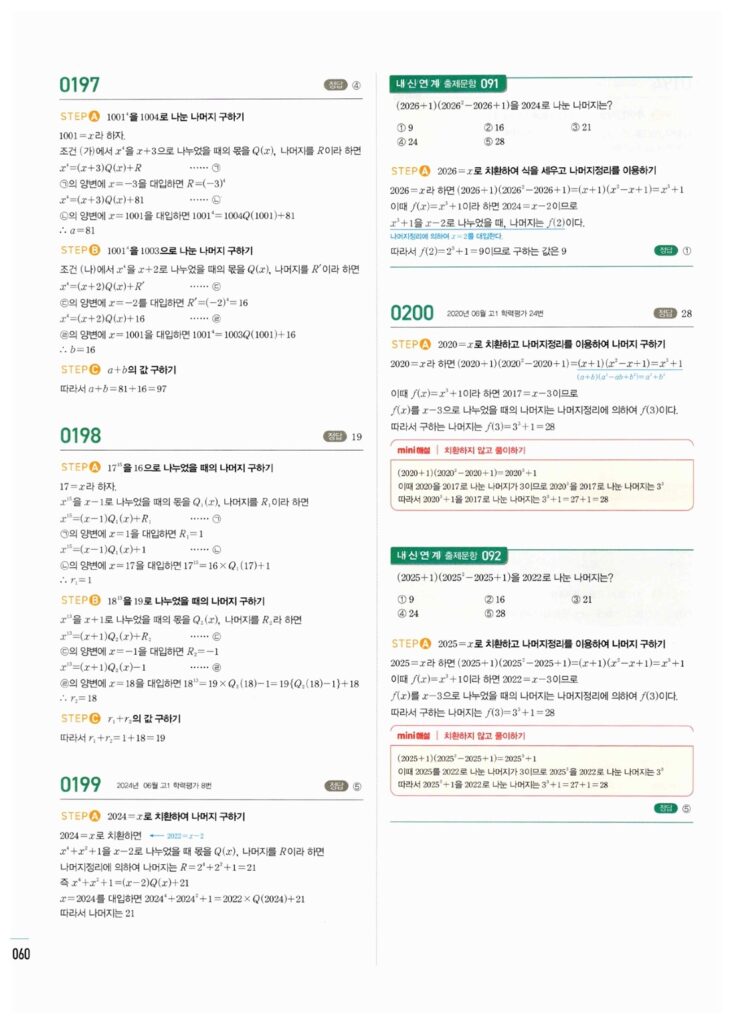
이번 파트의 핵심은 **나머지정리**입니다. 다항식 $P(x)$를 **1차식** $(x-\alpha)$로 나눌 때, 나머지가 $P(\alpha)$가 된다는 단순하지만 강력한 원리를 배우고 이를 문제에 적용합니다.
📌 나머지정리 공식의 핵심
나머지정리는 $P(x)$를 1차식으로 나눌 때만 바로 적용 가능합니다. 나눗셈에 대한 모든 문제는 **검산식 $\mathbf{P(x) = (x-\alpha)Q(x) + R}$**을 항등식으로 세우는 것부터 시작합니다. 나눗수가 0이 되는 $\mathbf{x=\alpha}$를 대입하면 몫($Q(x)$) 부분이 사라지고 나머지만 남게 됩니다.
📂 마플시너지 공통수학1 답지 전체 모음 & 필수 공식 다운로드 (클릭)
나머지정리는 $P(x)$를 1차식으로 나눌 때만 바로 적용 가능합니다. 나눗셈에 대한 모든 문제는 **검산식 $\mathbf{P(x) = (x-\alpha)Q(x) + R}$**을 항등식으로 세우는 것부터 시작합니다. 나눗수가 0이 되는 $\mathbf{x=\alpha}$를 대입하면 몫($Q(x)$) 부분이 사라지고 나머지만 남게 됩니다.
📖 나머지정리의 기본 활용 정답 및 해설
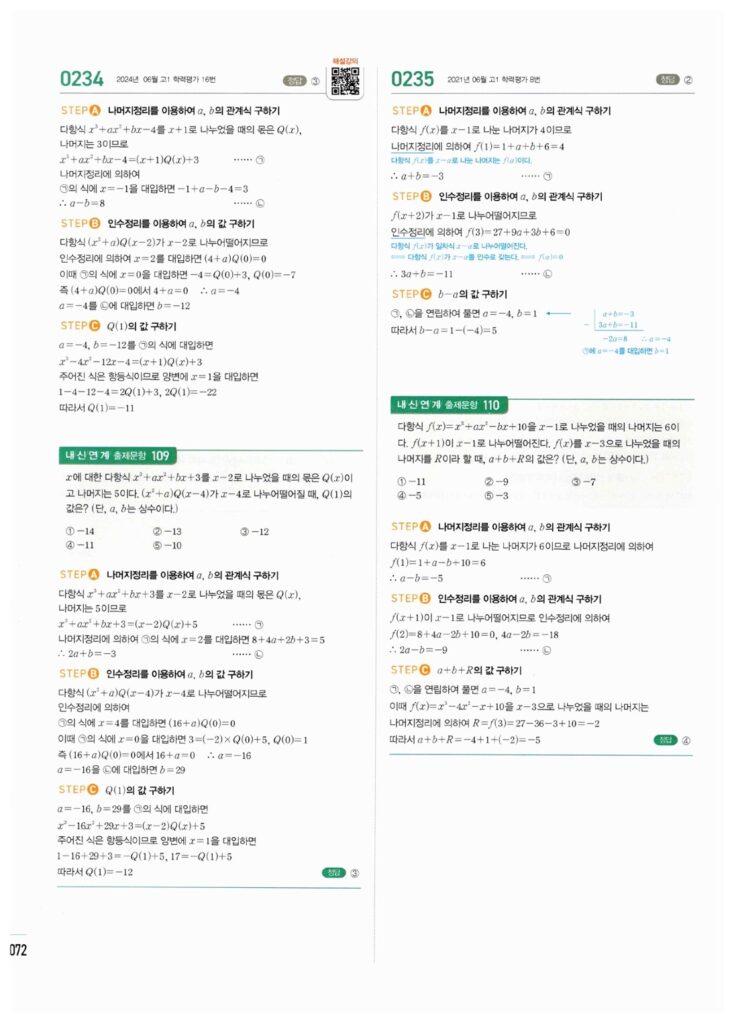
1차식으로 나눌 때 나머지를 구하는 문제와 미지수를 포함한 나머지정리 문제의 정답 이미지입니다. 이미지를 클릭(터치)하시면 확대됩니다.





💡 인수정리(Factor Theorem)의 이해
나머지정리의 특수한 경우로, 나머지가 0일 때를 **인수정리**라고 합니다. 즉, $P(\alpha) = 0$ 이면 $P(x)$는 $(x-\alpha)$로 나누어 떨어지고, $(x-\alpha)$는 $P(x)$의 **인수**가 됩니다. 이 원리는 다음 단원 **인수분해**의 핵심입니다.
현재 페이지: 1-2 항등식과 나머지정리 (2/3)