마플시너지 공통수학1 2-1 복소수 (1) 답지
안녕하세요. **마플시너지 공통수학1** **2-1 복소수** 첫 번째 파트(1/2) 정답 및 해설입니다. **허수 단위 $i$ ($i^2=-1$)**와 복소수 $a+bi$의 정의를 배우는 구간입니다.
복소수는 실수부와 허수부를 정확히 구분해야 하며, **$i$의 거듭제곱($i, -1, -i, 1$)이 4개를 주기로 반복**된다는 성질을 이용한 계산 문제가 출제됩니다.
[Image of powers of imaginary unit i periodicity]
📌 복소수 핵심: 실수와 허수의 구분
복소수 $a+bi$에서 $a$는 실수부, $b$는 허수부입니다. **$b=0$**이면 실수, **$b \ne 0$**이면 허수, 특히 **$a=0$이면서 $b \ne 0$**이면 순허수입니다. 이 분류를 정확히 아는 것이 중요합니다.
📂 마플시너지 공통수학1 답지 전체 모음 & 복소수 개념 특강 (클릭)
복소수 $a+bi$에서 $a$는 실수부, $b$는 허수부입니다. **$b=0$**이면 실수, **$b \ne 0$**이면 허수, 특히 **$a=0$이면서 $b \ne 0$**이면 순허수입니다. 이 분류를 정확히 아는 것이 중요합니다.
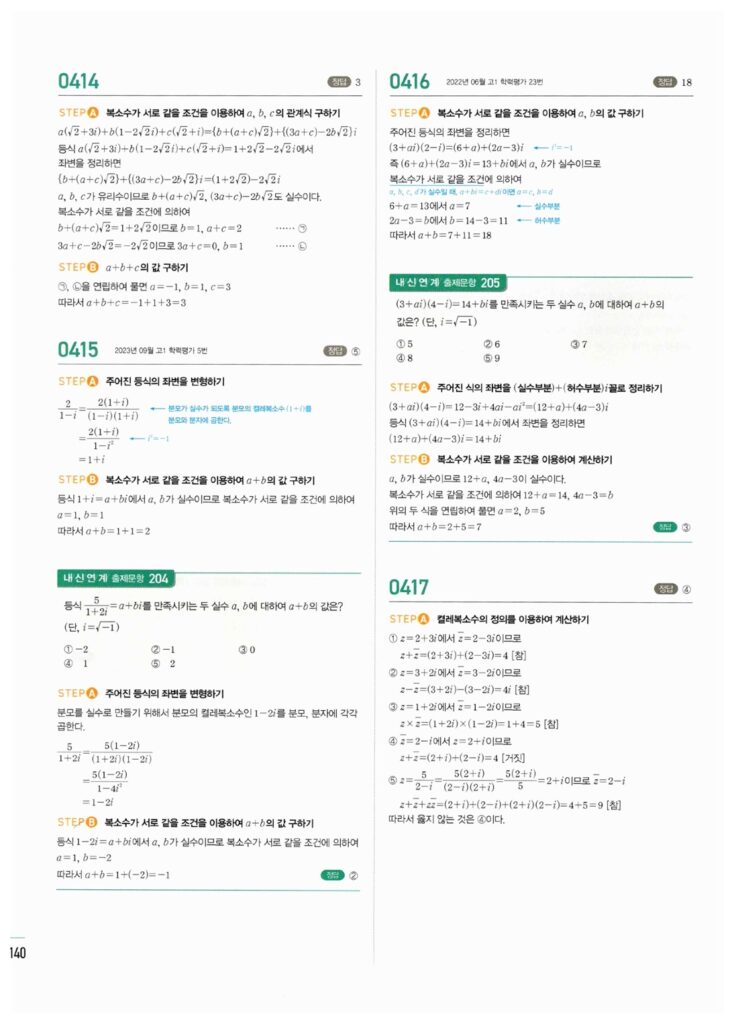
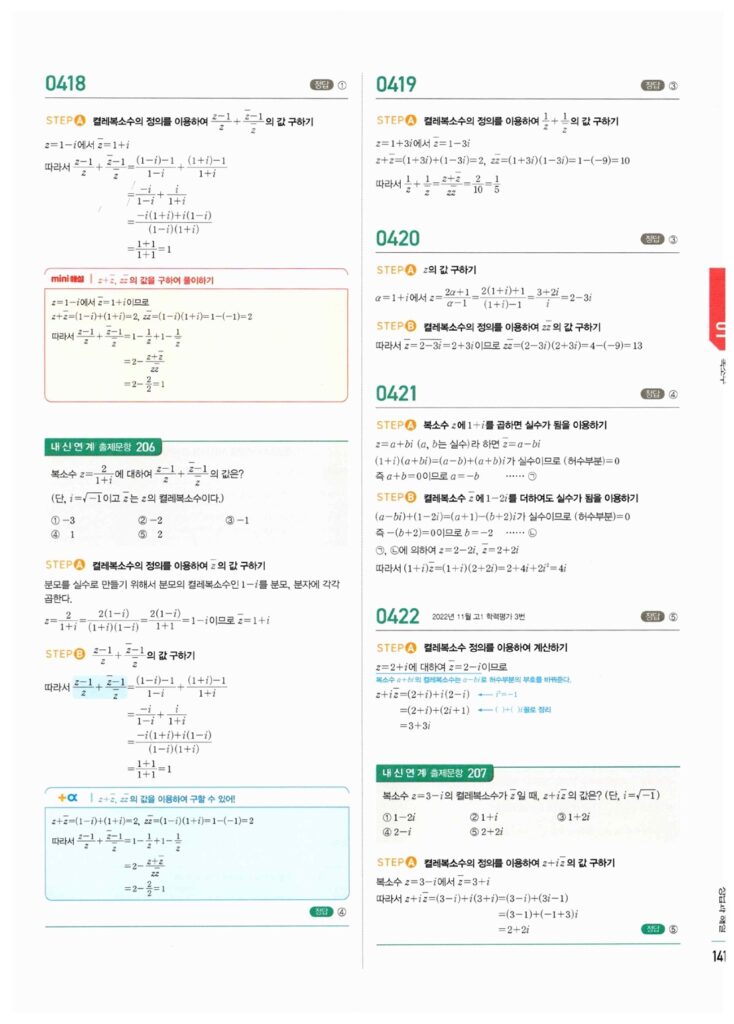
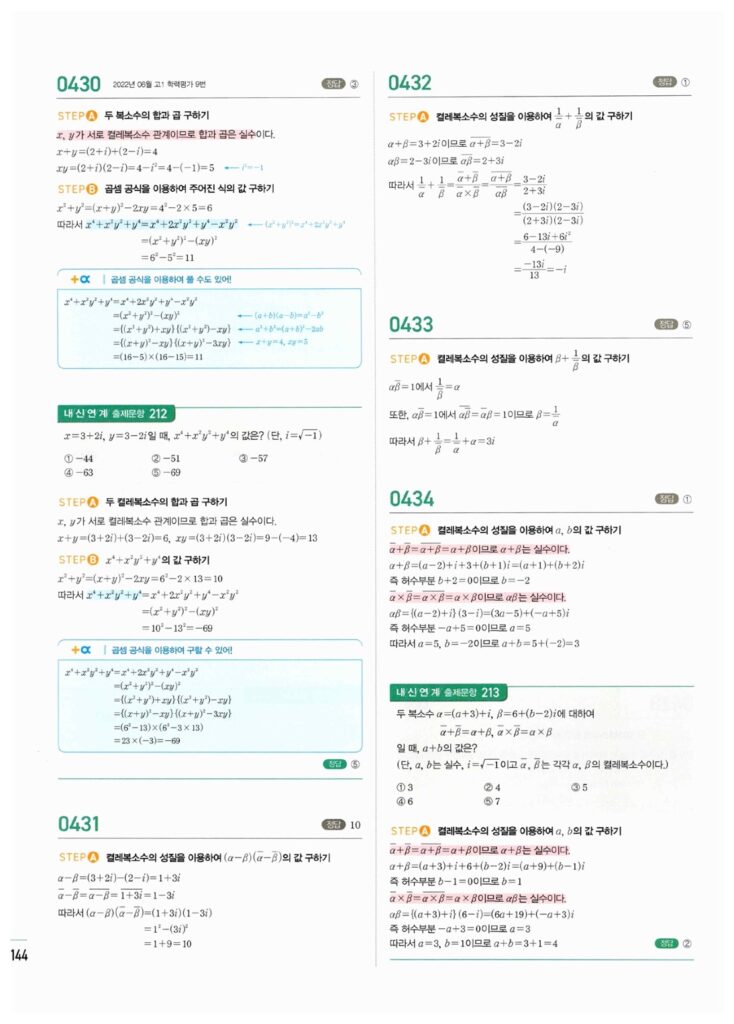
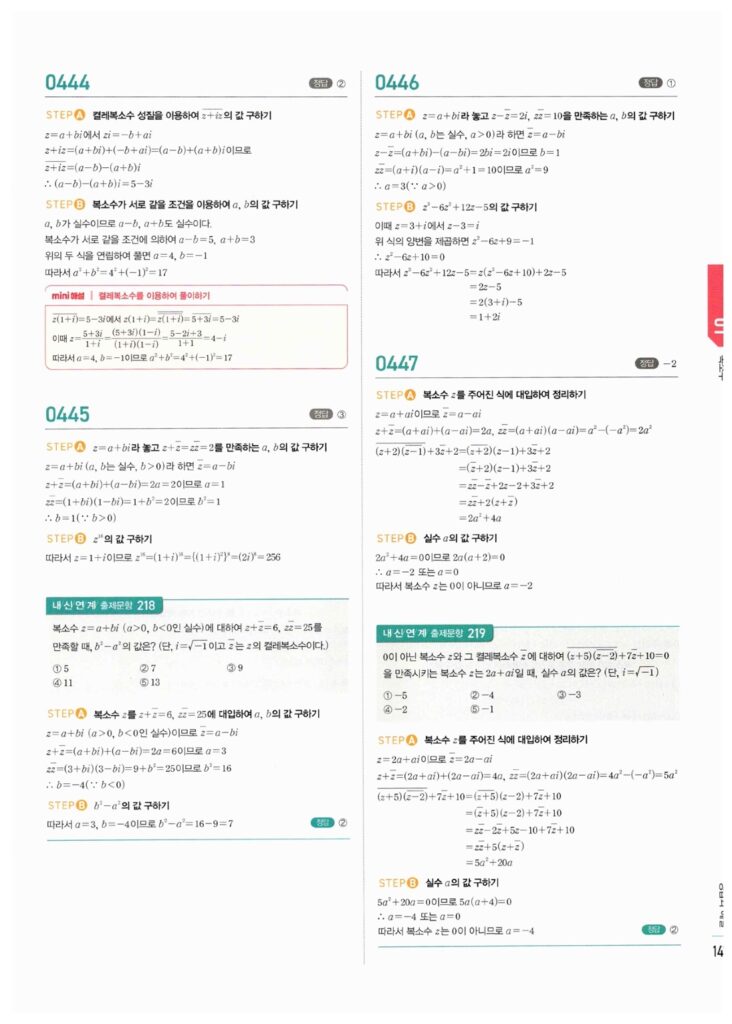
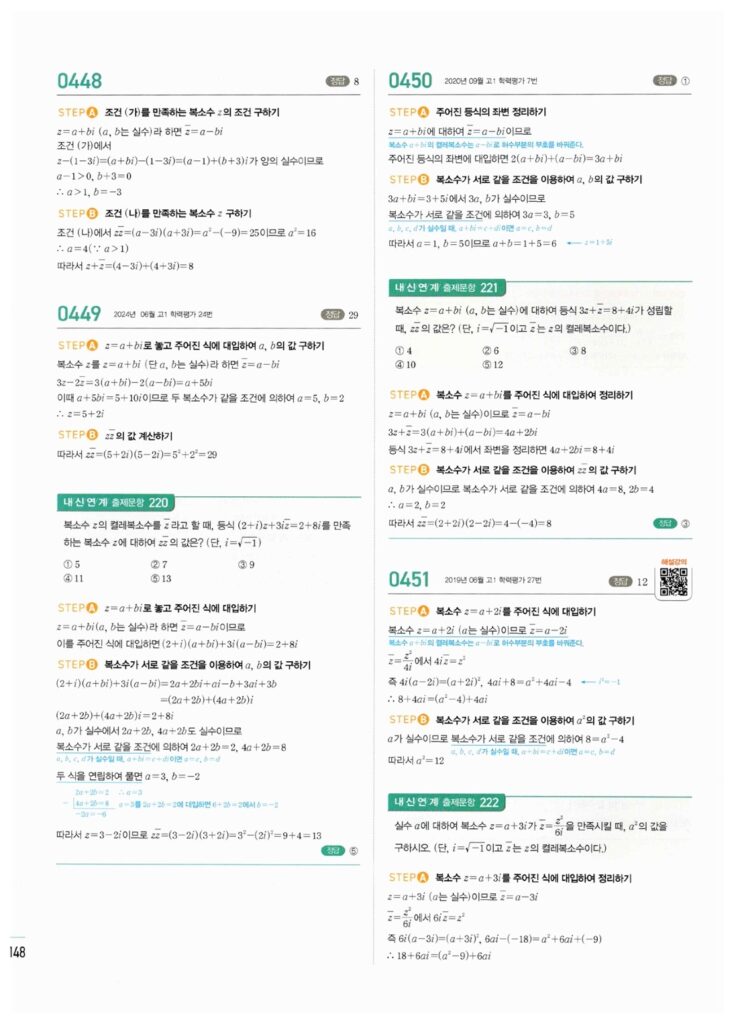
📖 복소수 (1) 정답 및 해설
복소수의 정의, $i$의 주기성, 복소수가 서로 같을 조건 문제의 정답 이미지입니다. 이미지를 클릭(터치)하시면 확대됩니다.




🎁 $i$의 거듭제곱, 4개씩 묶어 풀면 0이 된다는 사실!
$i+i^2+i^3+i^4$ 뿐만 아니라, $i^n+i^{n+1}+i^{n+2}+i^{n+3}$도 0입니다. **복잡한 $i$ 계산은 4개씩 끊어서 처리**하는 훈련을 하세요.
현재 페이지: 2-1 복소수 (1/2)