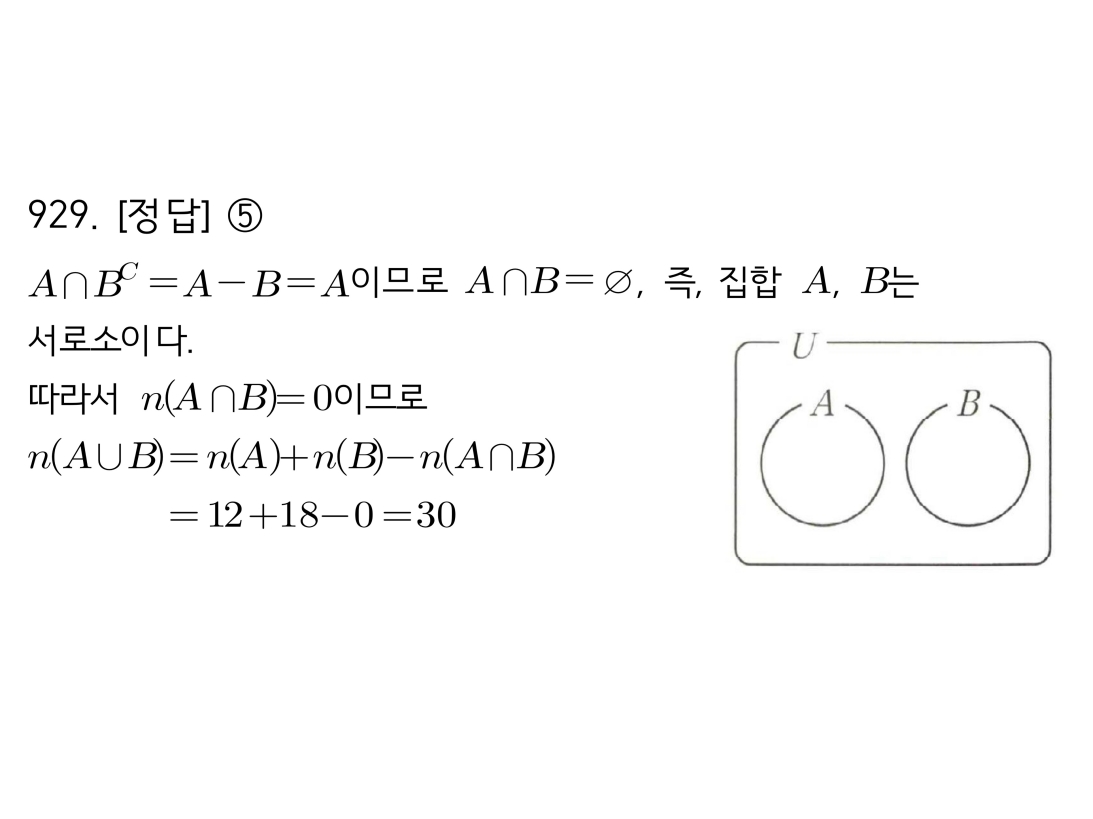
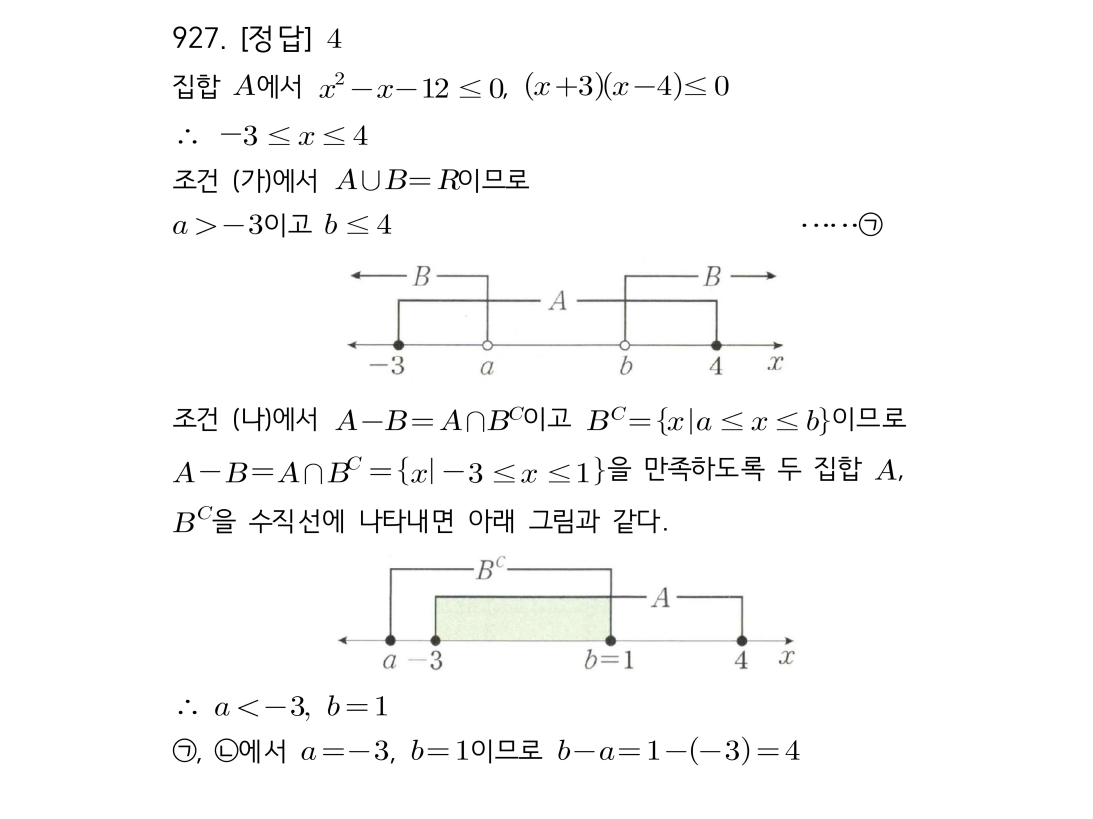
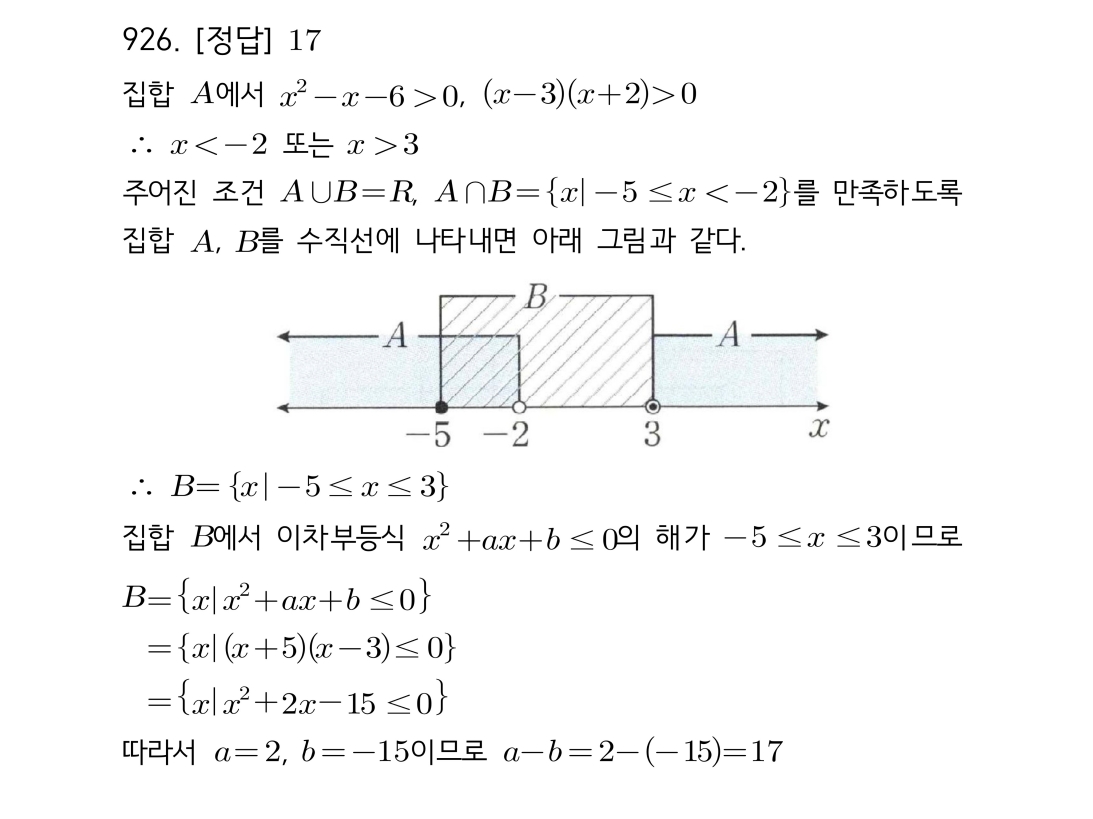
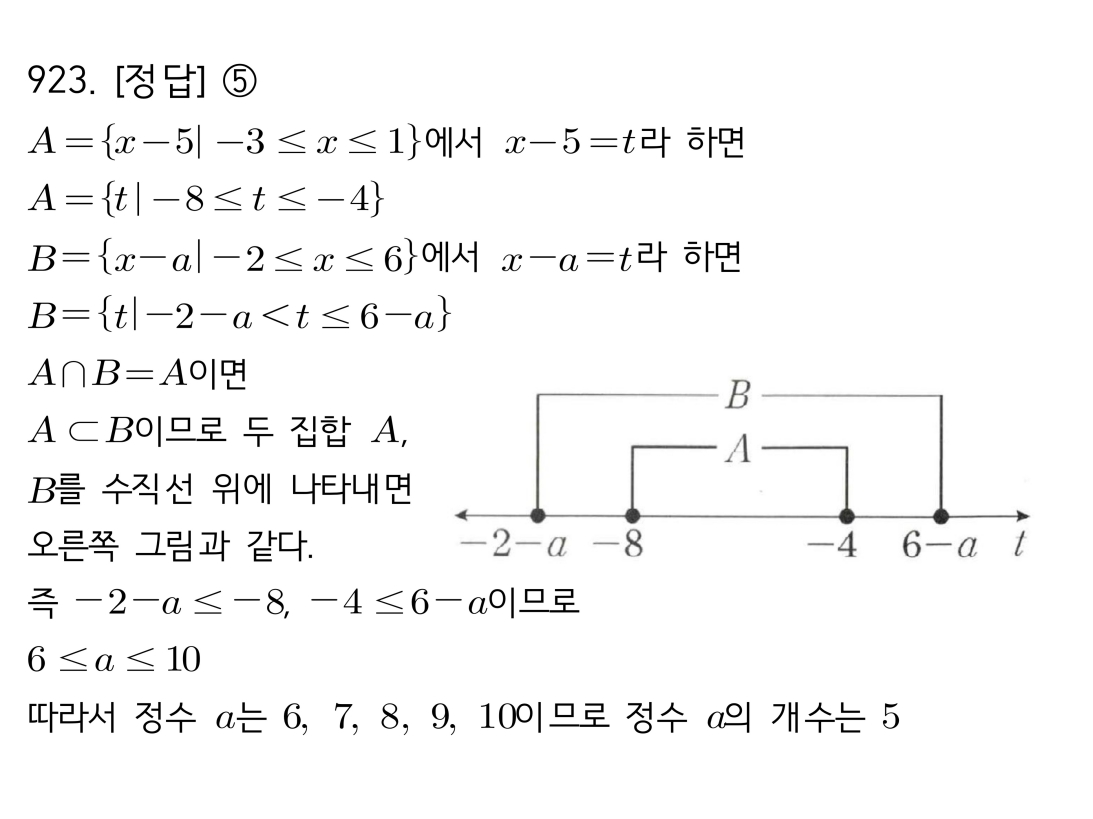
마플시너지공통수학2풀이해설0930고퀄리티 풀이영상제공0930 세 집합의 포함 관계로 필요/충분조건 찾기
“ [문제 930] 핵심 개념 및 풀이 전략 세 집합의 포함 관계를 통해 세 조건 사이의 필요/충분조건 관계를 파악하는 문제입니다. 접근법:1. R⊂(P∩Q) 라는 것은, R⊂P 이고 동시에 R⊂Q 임을 의미합니다.2. (r과 p의 관계) R⊂P 이므로 r→p는 참입니다. 따라서 r은 p이기 위한 **충분조건**입니다.3. (p와 q의 관계) P와 Q 사이의 포함 관계는 주어지지 않았으므로, 아무 관계도 아닙니다.4. … 더 읽기