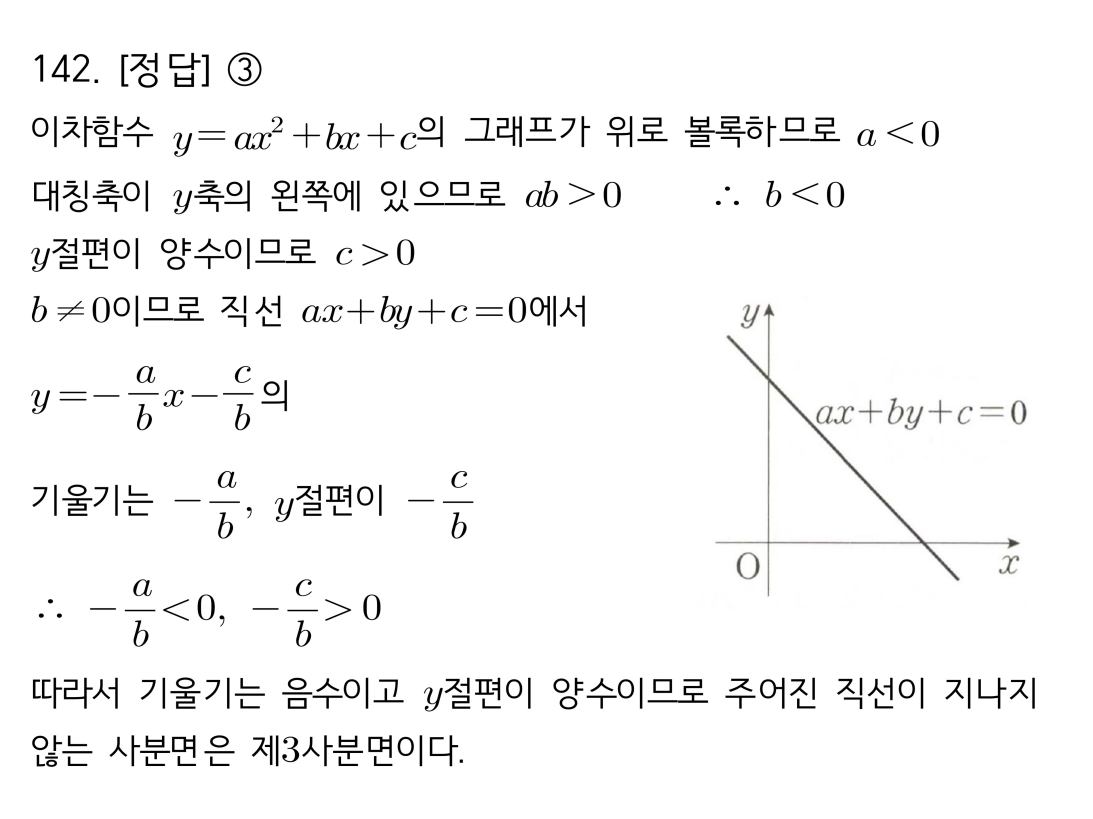
마플시너지공통수학2풀이해설0142고퀄리티 풀이영상제공0142 이차함수 계수 부호로 직선 추론
“ [문제 142] 핵심 개념 및 풀이 전략 이차함수의 그래프를 통해 계수 a, b, c의 부호를 판별하고, 이를 이용해 직선의 개형을 추론하는 융합 문제입니다. 접근법:1. (이차함수 분석) 위로 볼록하므로 a0), 따라서 b0.2. (직선 분석) 직선 ax+by+c=0의 기울기(-a/b)와 y절편(-c/b)의 부호를 1단계에서 얻은 정보로 판단합니다.3. ab>0 이므로 기울기 -a/b는 음수. bc