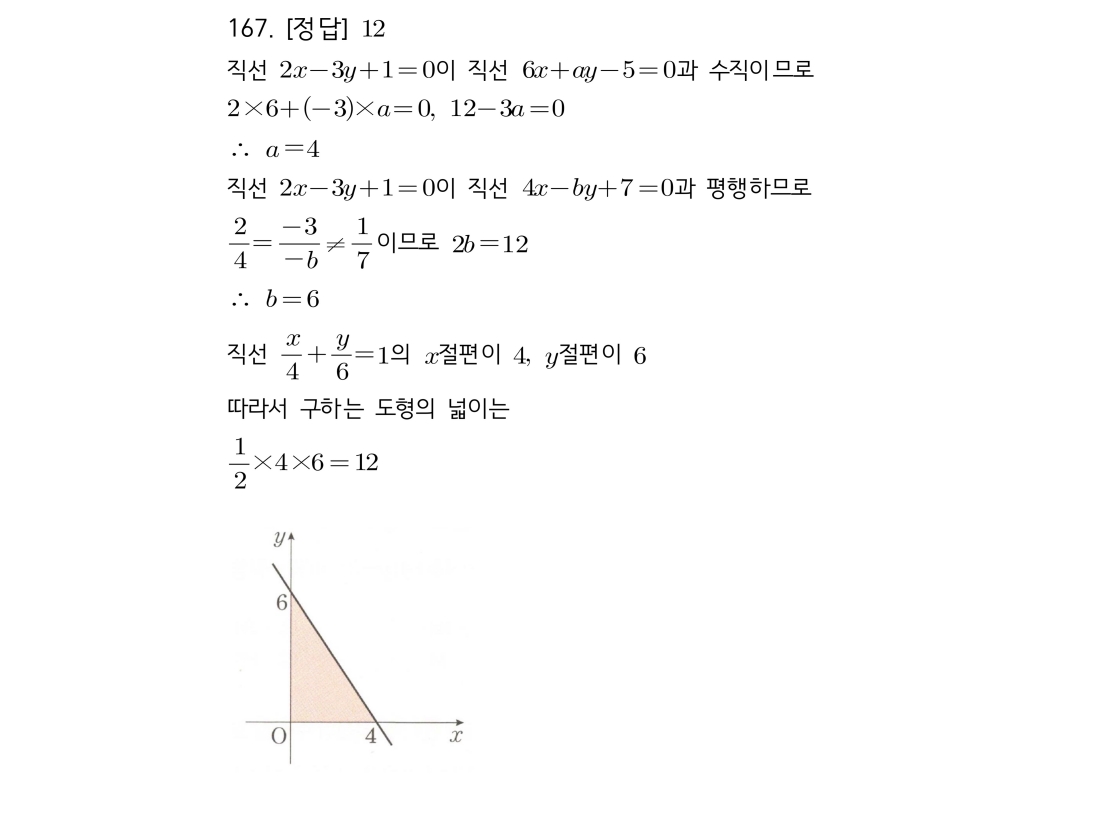
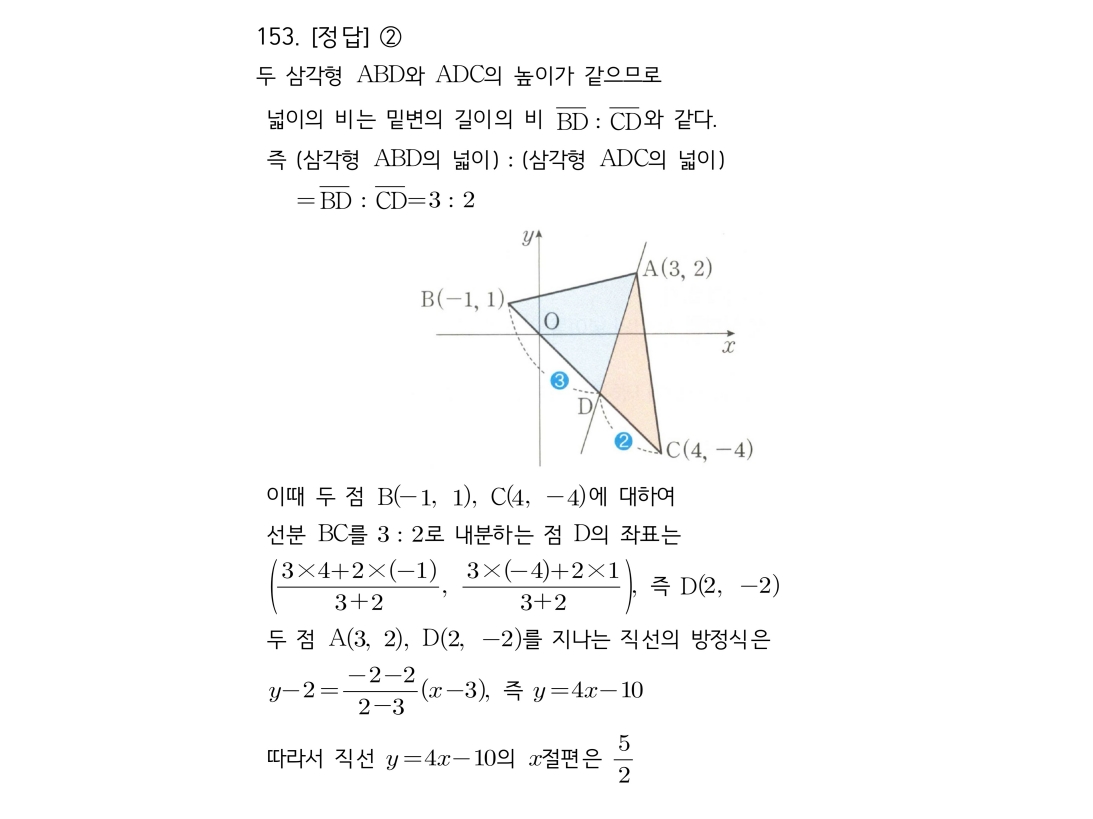
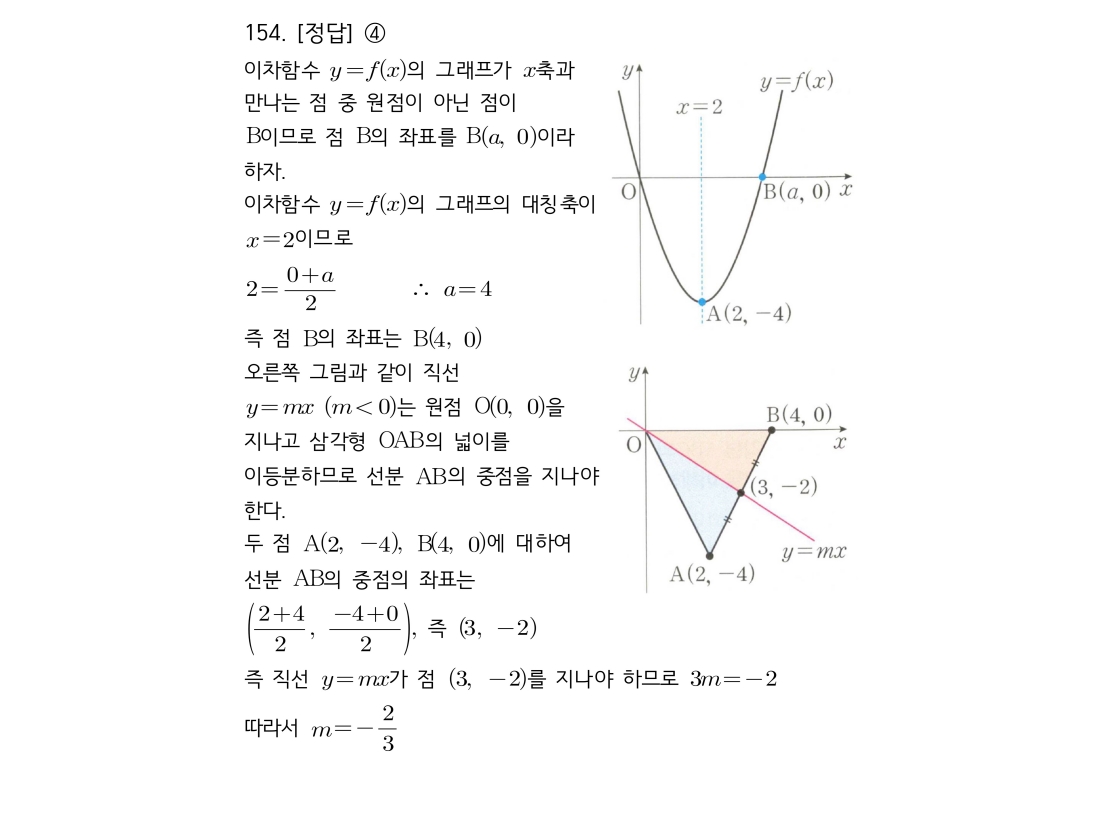
마플시너지공통수학2풀이해설0165고퀄리티 풀이영상제공0165 평행 조건과 수직 조건
“ [문제 165] 핵심 개념 및 풀이 전략 두 직선이 두 개 이상의 교점을 가질 조건을 묻는 문제입니다. 접근법:1. 서로 다른 두 직선이 두 개 이상의 교점을 갖는 경우는 오직 두 직선이 완전히 일치할 때뿐입니다.2. 두 직선이 일치할 조건, 즉 기울기와 y절편이 모두 같다는 조건을 식으로 표현합니다.3. 일반형 방정식에서의 일치 조건(a/a’ = b/b’ = c/c’)을 … 더 읽기