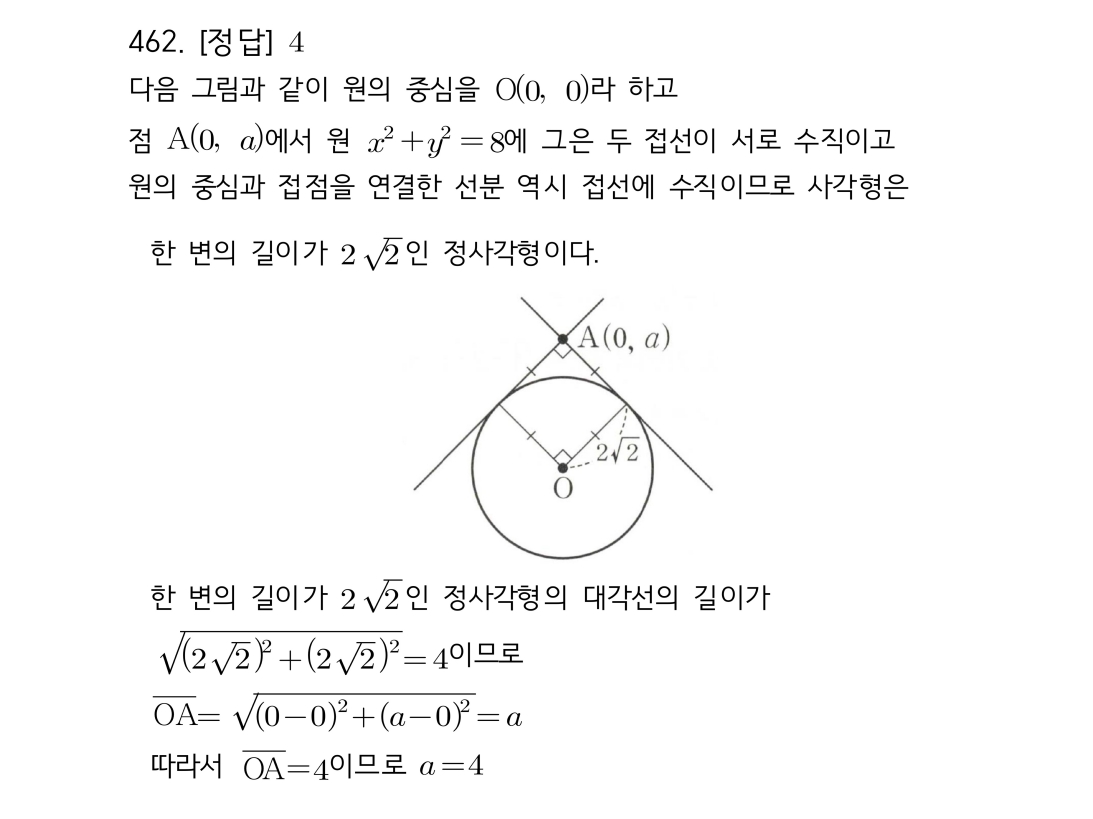
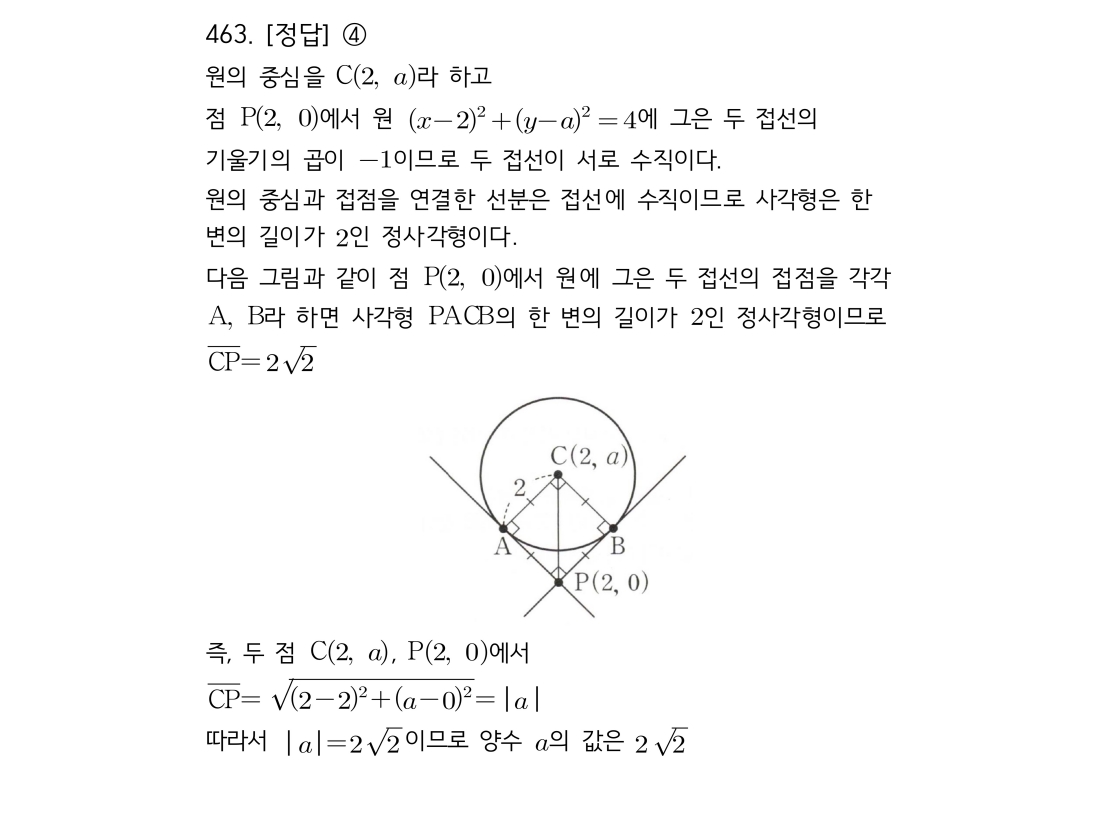
마플시너지공통수학2풀이해설0475고퀄리티 풀이영상제공0475 원과 직선 거리 최대/최소의 합
“ [문제 475] 핵심 개념 및 풀이 전략 원 위의 점과 직선 사이의 거리가 정수가 되도록 하는 점의 개수를 세는 문제입니다. 467번과 동일한 유형입니다. 접근법:1. 원의 중심 (1,-2)와 직선 x-y+3=0 사이의 거리 d를 구합니다.2. 원의 반지름 r은 √8 = 2√2 입니다.3. 원 위의 점에서 직선까지의 거리의 **최솟값 m = d-r** 과 **최댓값 M = d+r** … 더 읽기