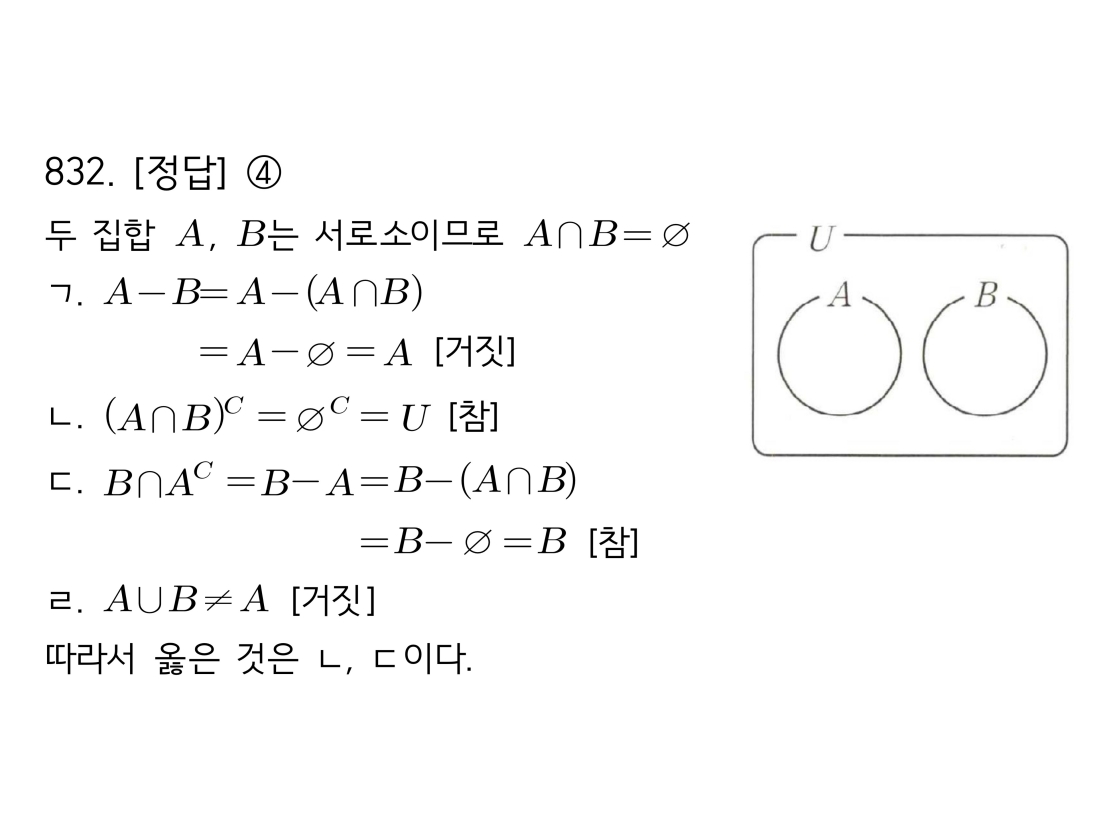
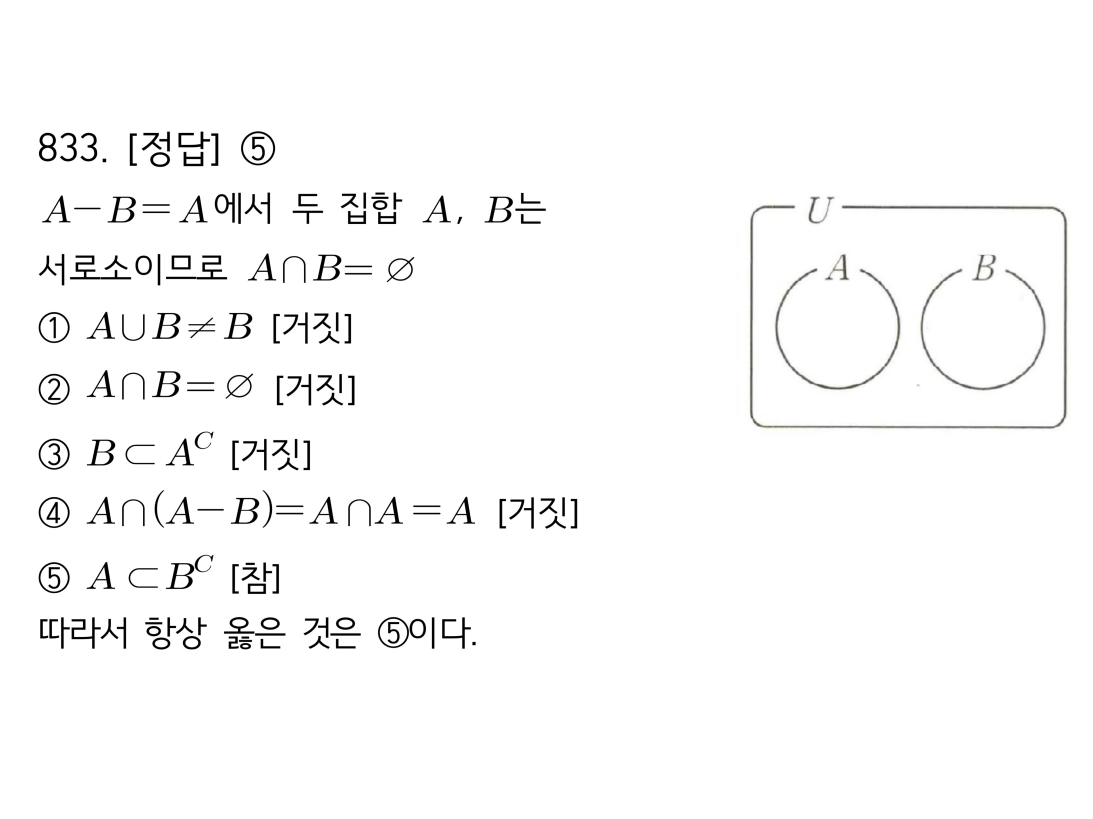
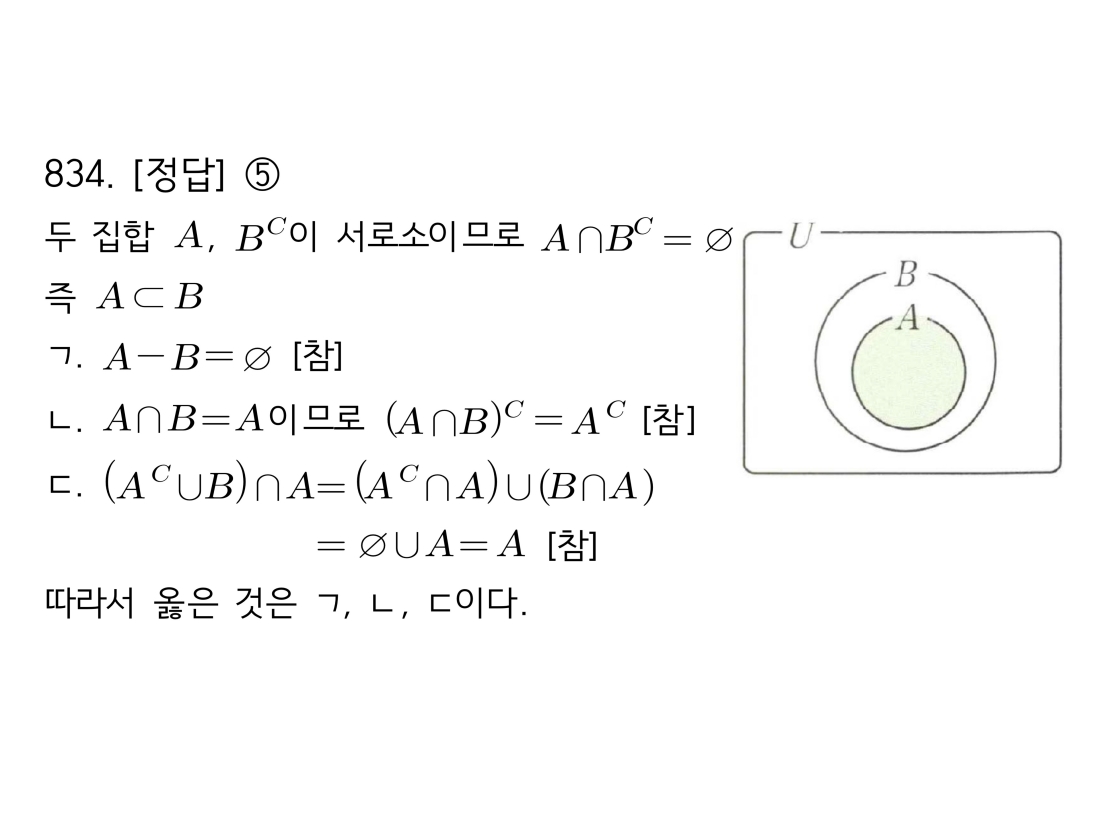
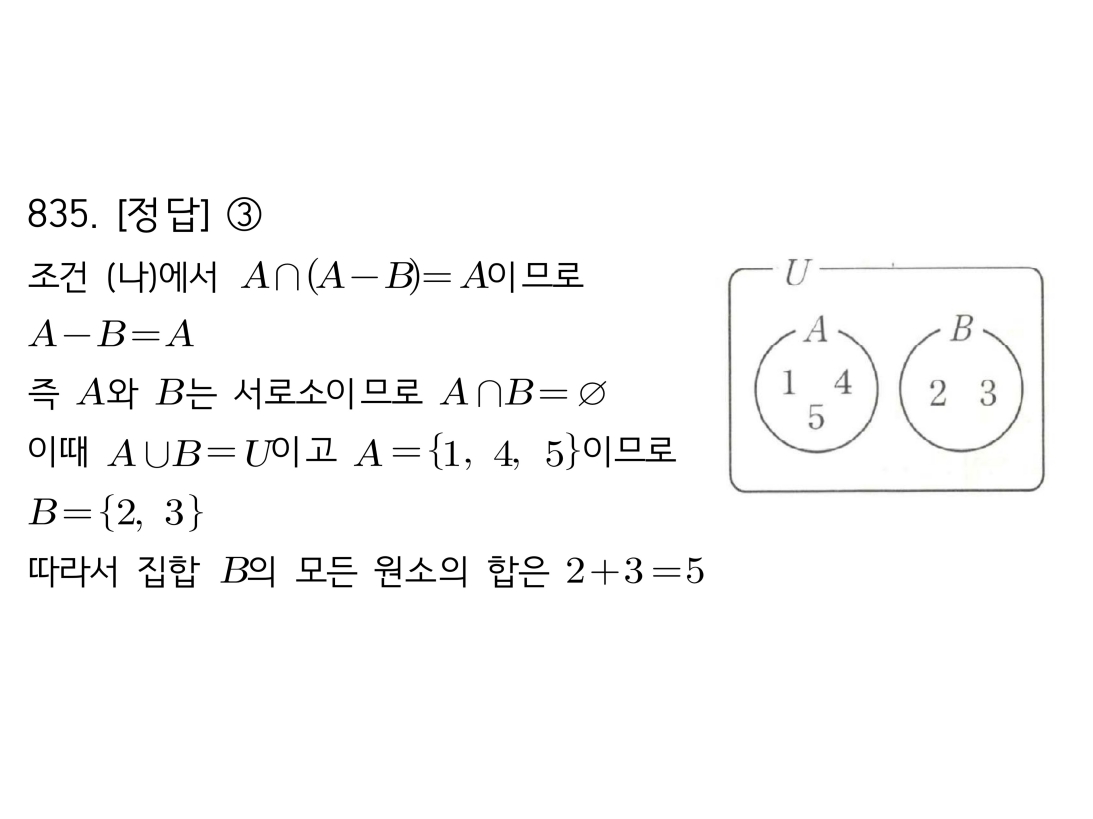
마플시너지공통수학2풀이해설0832고퀄리티 풀이영상제공0832 두 명제의 참/거짓과 집합의 관계
“ [문제 832] 핵심 개념 및 풀이 전략 주어진 집합 연산이 나타내는 벤 다이어그램 영역을 찾는 문제입니다. 접근법:1. 주어진 식 (B-A)ᶜ ∩ A 를 간단히 합니다.2. (B-A)ᶜ = (B∩Aᶜ)ᶜ = Bᶜ∪A (드모르간 법칙)3. (Bᶜ∪A) ∩ A = A 입니다. (흡수법칙)4. 따라서 주어진 식은 **집합 A** 전체를 의미합니다. A 영역이 색칠된 그림을 찾습니다. 주의할 점:흡수법칙 (X∪Y)∩X … 더 읽기