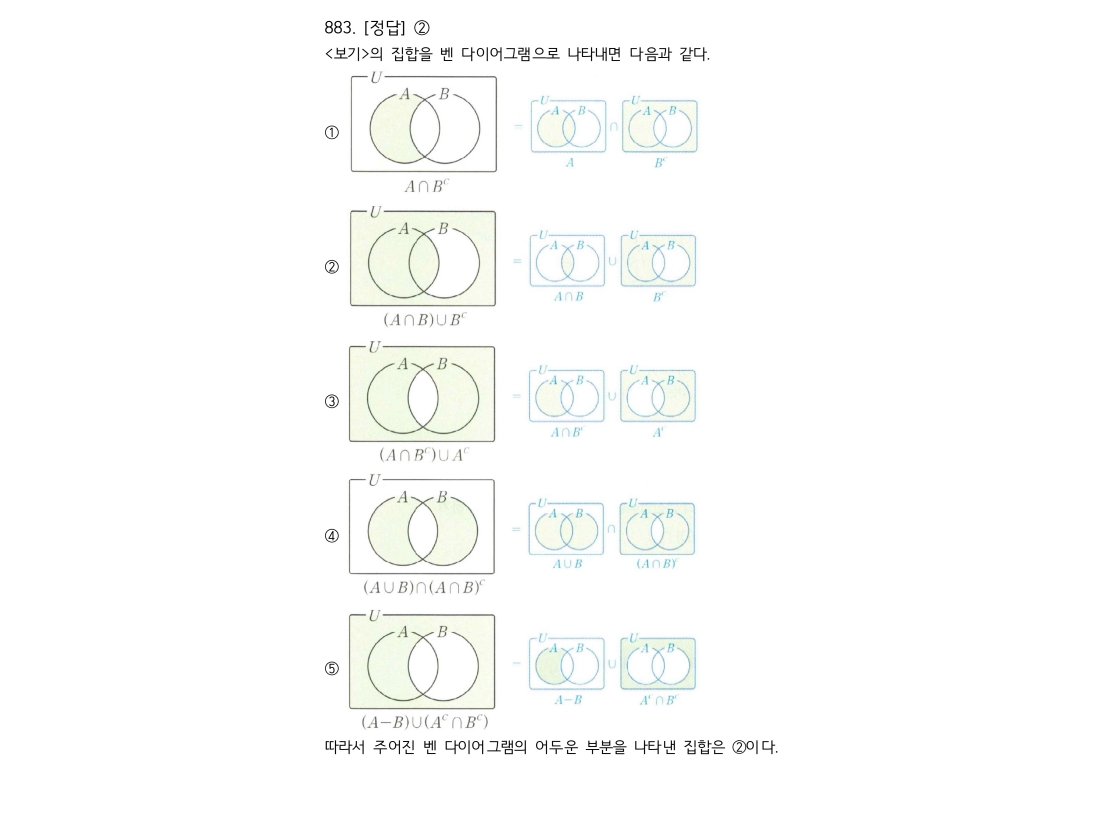
마플시너지공통수학2풀이해설0883고퀄리티 풀이영상제공0883 복잡한 집합 연산의 포함 관계 추론하기
“ [문제 883] 핵심 개념 및 풀이 전략 세 집합의 정보가 주어졌을 때, ‘한 가지 신문만 구독하는’ 가구 수를 구하는 서술형 문제입니다. 접근법:1. [1단계] ‘한 종류 신문만’ 구독하는 가구 수는 **n(A)+n(B)+n(C) – 2[n(A∩B)+n(B∩C)+n(C∩A)] + 3n(A∩B∩C)** 공식으로 구할 수 있습니다.2. [2단계] 주어진 정보 n(U), n(A), n(B), n(C), n(A∩B∩C), n((A∪B∪C)ᶜ)를 이용합니다.3. 먼저 n(A∪B∪C)를 구하고, 세 집합 합집합 … 더 읽기