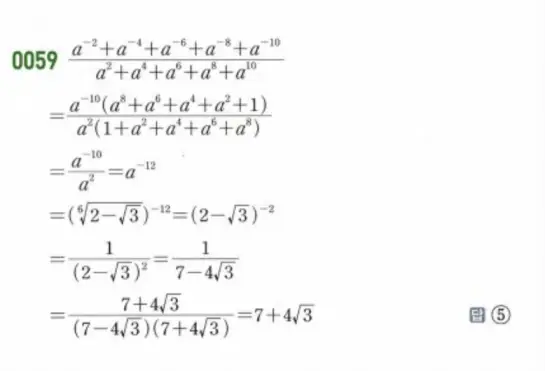
[쎈 대수] 0059번: 공식+꿀팁+영상! 복잡한 지수 식 10초 만에 푸는 법
안녕하세요! 여러분의 수학 성적을 확실하게 책임지는 친절하고 명쾌한 1타 강사 쌤입니다. 👋
지수 단원에서 항이 여러 개 나열된 분수식을 보면 숨부터 턱 막히는 친구들 많죠? 하지만 이런 문제일수록 ‘무작정 대입’이 아닌 ‘깔끔한 정리’가 정답입니다. 오늘 다룰 쎈 대수 0059번은 지수 법칙의 꽃이라고 할 수 있는 식의 구조 파악과 약분을 묻는 아주 세련된 문제입니다.
저는 실제 현장에서 학생들을 직접 가르치며 가장 반응이 좋고 효과적이었던 ‘최적의 풀이’만을 엄선해서 올리고 있습니다. 더 효율적인 풀이법이 발견된다면, 이 포스팅은 즉시 수정하고 업데이트될 예정이니 믿고 따라오세요! 😊
글로 된 설명보다 생생한 해설이 필요한 친구들은 포스팅 하단에 준비된 고퀄리티 해설 영상을 꼭 시청해 주세요. 자, 그럼 문제의 핵심을 찔러볼까요?
🧐 오늘의 문제 (쎈 대수 0059번)
\(a = \sqrt[6]{2-\sqrt{3}}\)일 때, 다음 식의 값을 구하시오.
① \(7-4\sqrt{3}\) ② \(2-\sqrt{3}\) ③ \(1\) ④ \(2+\sqrt{3}\) ⑤ \(7+4\sqrt{3}\)
💡 핵심 분석 & 필수 공식
이 문제를 풀기 위해 \(a\) 값을 처음부터 대입하는 것은 ‘계산 지옥’으로 가는 길입니다. 먼저 식을 간단히 하기 위한 지수 법칙과 인수분해가 필요합니다. 📝
2. 지수의 확장: \((a^m)^n = a^{mn}\)
3. 공통인수 묶기: 분자와 분모에서 차수가 가장 낮거나 높은 항으로 묶어 식을 대칭 구조로 만듭니다.
📸 이미지로 보는 단계별 상세 풀이
아래 공간에 직접 작성하신 고퀄리티 이미지 해설을 업로드해 주세요.
이미지 해설 포인트:
1. 분자를 \(a^{-10}\)으로, 분모를 \(a^2\)으로 묶어 공통부분 \((1+a^2+a^4+a^6+a^8)\)을 만듭니다.
2. 약분 후 남은 \(a^{-12}\)에 문제의 \(a\) 값을 대입하여 계산합니다.
🍯 쌤의 1등급 꿀팁 & 실수 포인트
🚫 [주의! 실수 포인트]
마지막 단계에서 \((2-\sqrt{3})^{-2}\)를 계산할 때, 단순히 부호를 바꾸는 실수를 하면 안 돼요! 지수의 마이너스는 ‘역수’를 의미합니다. 즉, \(\frac{1}{(2-\sqrt{3})^2}\)으로 계산한 후 유리화까지 완벽하게 마쳐야 정답 ⑤번에 도달할 수 있습니다.
💡 [쌤의 꿀팁]
이런 대칭형 분수식은 “분자의 최저차항과 분모의 최저차항의 차이”만 보면 끝납니다. 분자의 최저차 \(a^{-10}\)과 분모의 최저차 \(a^2\)를 나눈 \(a^{-12}\)이 바로 남는 값이 되죠. 이 비법만 알면 시험에서 1분 컷 가능합니다! ⚡
🎓 마무리하며
오늘 풀어본 쎈 대수 0059번은 복잡한 겉모습에 속지 않고 수학적 구조를 읽어내는 능력을 키워주는 문제입니다. 연습장에 직접 공통인수를 묶어 약분하는 과정을 꼭 한 번 그려보세요.
글로 다 전하지 못한 명쾌한 판서 해설과 상세 노하우는 바로 아래 영상에 담았습니다. 🎬 이해가 100% 되지 않았다면 영상을 시청하며 부족한 부분을 채워보세요. 여러분의 수학 1등급을 언제나 응원합니다! 화이팅! 👊
- 본 블로그에 게시된 모든 자료(답지 및 해설)의 저작권은 해당 교재의 출판사에 있습니다.
- 자료는 오직 학생들의 채점, 오답 정리, 자기주도 학습용으로만 활용해 주시기 바랍니다.
- 제공된 파일을 상업적으로 이용하거나, 타 사이트에 무단 배포하여 발생하는 모든 법적 책임은 이용자 본인에게 있습니다.
- 저작권 관련 문제가 있거나 삭제를 원하시는 출판사 관계자분께서는 [leinbow@gmail.com]로 연락 주시면 즉시 조치하겠습니다.