쎈 공통수학1 0054번 풀이
(5x+ay)³ 전개식에서 xy²의 계수 조건으로 x²y의 계수 구하기
유형 03 · 곱셈공식을 이용한 전개 난이도 ⭐중 📝 서술형📋 이 포스팅에 포함된 내용
- 풀이 영상 (동영상 해설)
- 해설 이미지 (쎈 공통수학1 답지)
- 문제 분석 및 단서 찾기
- 단계별 상세 풀이 (서술형 답안 작성법 포함)
- 꿀팁: 외워두면 좋은 패턴
- 흔한 실수 & 주의사항
- 시간 관리 전략
- 관련 개념 및 추천 링크
🎬 풀이 영상
서술형 답안 작성법까지 함께 확인하세요! 영상 먼저 보고 아래 풀이로 복습하면 좋아요.
🔍 문제 분석 — 단서 찾기
다항식 (5x + ay)³의 전개식에서 xy²의 계수가 60일 때, x²y의 계수를 구하시오. (단, a > 0)
🔑 핵심 단서 포인트
📝 단계별 상세 풀이
Step 1. 세제곱 공식으로 전개하기 50%
(a+b)³ = a³ + 3a²b + 3ab² + b³ 공식에서 a = 5x, b = ay를 대입:
각 항을 정리하면:
각 항의 계수 정리
· x³의 계수: 125
· x²y의 계수: 75a
· xy²의 계수: 15a²
· y³의 계수: a³
Step 2. xy²의 계수 조건으로 a 구하기 30%
xy²의 계수가 60이므로:
a² = 4
a = 2 (∵ a > 0)
Step 3. x²y의 계수 구하기 20%
a = 2를 x²y의 계수 75a에 대입:
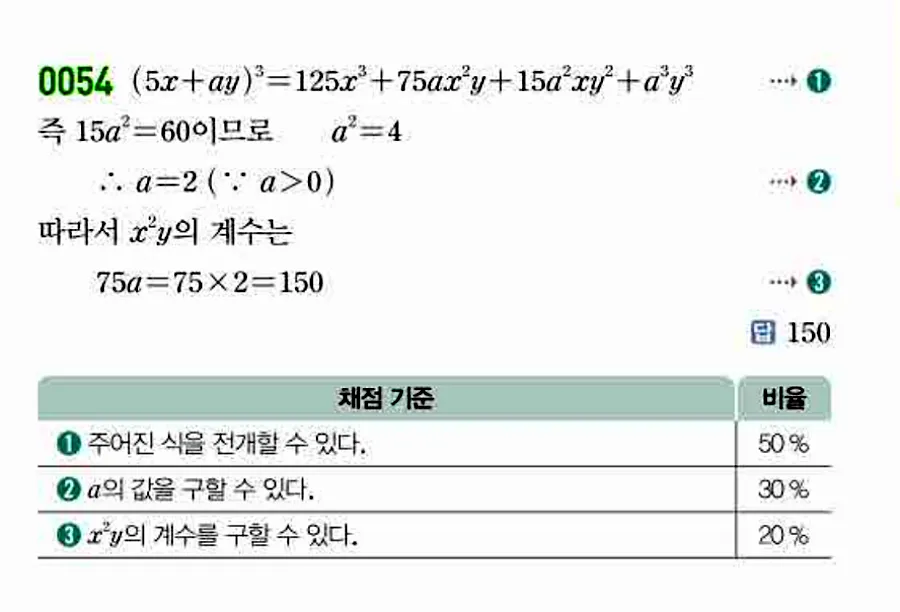
📸 해설 이미지 (쎈 공통수학1 답지)
아래 이미지에서 0054번 풀이를 직접 확인해 보세요.
🍯 꿀팁 & 외워두면 좋은 패턴
(Ax + By)³ 전개 — 계수 빠르게 구하는 법
(Ax + By)³의 전개식 각 항의 계수:
· x³의 계수: A³
· x²y의 계수: 3A²B
· xy²의 계수: 3AB²
· y³의 계수: B³
🔥 공식 계수 1, 3, 3, 1에 A와 B의 거듭제곱을 곱하면 끝!
“조건으로 미지수 구하기 → 원하는 값 계산” 2단계 패턴
이런 문제는 항상 같은 흐름이에요:
① 전개 공식 적용 → 각 항의 계수를 미지수(a)로 표현
② 주어진 조건(계수 = 60)으로 미지수 a 결정
③ 구한 a를 원하는 항의 계수에 대입
🔥 이 3단계만 기억하면 서술형도 완벽하게 풀 수 있어요!
서술형 답안 작성 Tip
서술형에서는 풀이 과정이 곧 점수예요! 위의 Step 1~3처럼 단계를 나눠서 쓰면:
· Step 1 (전개) → 부분 점수 50%
· Step 2 (a 구하기) → 부분 점수 30%
· Step 3 (최종 답) → 나머지 20%
설령 최종 답을 틀려도, 전개 과정만 맞으면 부분 점수를 받을 수 있어요!
⚠️ 흔한 실수 & 주의사항
실수 1: a² = 4에서 a = ±2로 두고 조건을 무시
a² = 4이면 a = ±2이지만, 문제에서 a > 0 조건이 있으므로 a = 2만 가능해요. 조건을 꼭 확인하세요!
실수 2: 공식 계수 3과 A, B의 계수를 혼동
3(5x)²(ay)를 계산할 때:
· (5x)² = 25x²
· 3 × 25 × a = 75a
이 과정에서 25를 5로 잘못 쓰거나, 3을 빼먹는 실수를 자주 해요!
실수 3: xy²과 x²y를 혼동
조건에서 주어진 것은 xy²의 계수이고, 구해야 하는 것은 x²y의 계수예요. 이 두 항을 바꿔서 계산하면 처음부터 틀리게 돼요!
⏱️ 시간 관리 전략
목표 풀이 시간
내신 시험 (서술형): 4~5분 (풀이 과정을 깔끔하게 적는 시간 포함)
수능/모의고사: 2~3분
시간을 줄이려면?
📚 더 공부하기 — 추천 순서
📝 연산 워크시트 (기초 다지기)
공통수학1 연산 05. 곱셈 공식 (1) 공통수학1 연산 06. 곱셈 공식 (2) 공통수학1 연산 07. 곱셈 공식의 변형 공통수학1 연산 03. 다항식의 곱셈 (1) 공통수학1 연산 04. 다항식의 곱셈 (2)📖 관련 개념 포스트
개념사전 008. 곱셈공식 정리 개념사전 006. 식 전개하기 개념사전 009. 곱셈공식의 변형 활용 개념사전 005. 지수의 법칙 개념사전 007. 다항식 곱셈의 연산법칙🚀 마플시너지 공통수학1 (심화 도전)
마플시너지 0073번 | 다항식 곱셈 완벽정리 마플시너지 0058번 | 항등식 특수값 대입 빠른풀이 마플시너지 097번 | 항등식 계수비교 마플시너지 098번 | 부정계수법 다항식나눗셈
💪 서술형은 풀이 과정이 곧 점수!
“전개 → 조건으로 미지수 결정 → 원하는 값 계산” 3단계를 깔끔하게 쓰면
부분 점수도 확실히 챙길 수 있어요! 화이팅! 🎯