📚 쎈 공통수학1 답지 0042번 – 다항식 곱셈과 덧셈 혼합 완벽 해설
✨ 이 포스팅에 담긴 내용
- ✅ 쎈 공통수학1 0042번 문제 해설 이미지
- 🎥 문제 풀이 동영상 (유튜브)
- 📝 단계별 자세한 풀이 과정
- 💡 핵심 개념과 실수 방지 팁
- ⏱️ 시험 시간 관리 전략
- 🔗 관련 개념 학습 링크
📌 문제 분석
[쎈 공통수학1 0042번 문제 요약]
두 다항식 A, B가 주어졌을 때, 곱셈식과 덧셈식이 혼합된 복합 연산 문제입니다.
- A = x² + 2x – y + 1
- B = 2x – y – 5
- 계산식: A × B = 3A – B를 만족할 때, (x² + 2x – y + 1) × (2x – y – 5)를 계산
💡 핵심 포인트
두 다항식의 곱셈은 분배법칙을 두 번 적용!
첫 번째 다항식의 각 항에 두 번째 다항식 전체를 곱한 후, 모든 항을 전개합니다.
이 문제는 기본 곱셈 계산 문제로, 정확성이 가장 중요합니다.
📖 해설 이미지
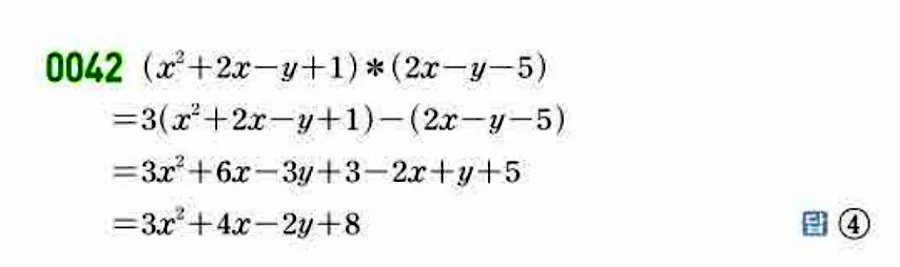
🎥 풀이 동영상
📝 단계별 풀이
STEP 1: 곱셈 전략 세우기
주어진 식: (x² + 2x – y + 1) × (2x – y – 5)
이 문제의 핵심은 각 항을 빠짐없이 곱하는 것입니다.
곱셈 공식:
첫 번째 다항식의 4개 항 × 두 번째 다항식의 3개 항 = 총 12개 항이 나옵니다!
이 문제의 단서는 “두 다항식의 곱셈”입니다.
곱셈을 정확하게 하려면:
- 첫 번째 다항식을 항별로 분리: x², 2x, -y, 1
- 각 항에 두 번째 다항식 전체를 곱함:
- x² × (2x – y – 5)
- 2x × (2x – y – 5)
- -y × (2x – y – 5)
- 1 × (2x – y – 5)
- 모든 결과를 더함
STEP 2: 각 항별로 곱셈 계산하기
① x² × (2x – y – 5)를 계산:
x² × (-y) = -x²y
x² × (-5) = -5x²
② 2x × (2x – y – 5)를 계산:
2x × (-y) = -2xy
2x × (-5) = -10x
③ (-y) × (2x – y – 5)를 계산:
-y × (-y) = y²
-y × (-5) = 5y
④ 1 × (2x – y – 5)를 계산:
1 × (-y) = -y
1 × (-5) = -5
⚠️ 이 문제에서 학생들이 가장 어려워하는 부분
“항이 많아서 빠뜨리거나 부호를 틀리는 것!”
- 항 개수 확인: 4개 × 3개 = 12개의 항이 나와야 합니다
- 부호 주의:
- 양수 × 양수 = 양수
- 양수 × 음수 = 음수
- 음수 × 음수 = 양수 (특히 -y × (-y) = y²)
- xy항이 두 번 나옴: -2xy가 두 번 나오므로 나중에 -4xy가 됩니다
- x²항도 여러 개: -5x²과 4x²를 합쳐야 합니다
항을 빠뜨리면 답이 완전히 틀립니다! 체계적으로 하나씩 곱하세요.
STEP 3: 모든 항 나열하기
위에서 계산한 12개의 항을 모두 나열하면:
STEP 4: 동류항끼리 정리하기
이제 같은 종류의 항끼리 모아서 정리합니다:
| 항의 종류 | 계산 과정 | 결과 |
|---|---|---|
| x³항 | 2x³ | 2x³ |
| x²y항 | -x²y | -x²y |
| x²항 | -5x² + 4x² | -x² |
| xy항 | -2xy – 2xy | -4xy |
| y²항 | y² | y² |
| x항 | -10x + 2x | -8x |
| y항 | 5y – y | 4y |
| 상수항 | -5 | -5 |
📌 동류항 정리 체크리스트
다항식 곱셈 후에는 다음 순서로 정리하세요:
- 차수가 가장 높은 항부터 (x³ → x²y → x² → …)
- 같은 차수에서는 x의 차수가 높은 것부터
- 각 항의 개수를 세어 빠진 것이 없는지 확인
- 부호를 다시 한 번 확인
🎯 외워두면 좋은 패턴
📌 다항식 곱셈 패턴
- 항 개수 계산
- (a항)(b항) = a×b개의 항이 나옴
- 4개 항 × 3개 항 = 12개 항
- 체계적으로 곱하기
- 첫 번째 다항식의 첫 번째 항부터 차례대로
- 각각에 두 번째 다항식 전체를 곱함
- 표로 정리하기
- 가로에 첫 번째 다항식의 항
- 세로에 두 번째 다항식의 항
- 교차하는 칸에 곱셈 결과
- 동류항 정리는 차수순으로
- 최고차항부터 차례대로
- 같은 문자와 차수끼리 모음
⏱️ 시험 시간 관리
⏰ 이 문제를 풀어야 하는 시간
| 시험 유형 | 목표 시간 | 난이도 |
|---|---|---|
| 내신 시험 (학교 시험) | 3~4분 | 중 |
| 수능 모의고사 | 2.5~3.5분 | 중 |
⚡ 시간을 줄이려면?
- 표 활용: 곱셈표를 그려서 빠짐없이 체계적으로 계산
- 동류항 미리 예상: xy항이 여러 개 나올 것을 미리 알고 표시
- 부호 계산 정확도: 음수끼리 곱할 때 양수가 되는 것 주의
- 검산은 상수항: -5만 나오므로 빠르게 확인 가능
- 선택지 활용: 최고차항(x³)의 계수를 먼저 확인
💡 정확도가 속도보다 중요!
이 문제는 항이 많아서 실수하기 쉬운 문제입니다.
빨리 풀려다가 항을 빠뜨리면 처음부터 다시 풀어야 하므로,
천천히 정확하게 푸는 것이 결국 더 빠릅니다!
🔗 관련 개념 포스팅
🔢 연산 연습
• 다항식 곱셈 기본 연습 • 두 다항식의 곱셈 드릴 • 곱셈 후 동류항 정리 연습 • 부호 계산 집중 훈련 • 문자 2개 다항식 곱셈📚 다항식 기본 개념
• 다항식의 곱셈 원리 • 분배법칙의 확장 • 동류항의 정의와 정리 • 곱셈 후 차수 결정하기 • 두 문자 다항식의 이해📖 마플시너지 공통수학1 추천 문제
• 마플시너지 공통수학1 – 다항식 곱셈 기본 • 마플시너지 공통수학1 – 두 다항식의 곱 계산 • 마플시너지 공통수학1 – 곱셈과 덧셈 혼합 • 마플시너지 공통수학1 – 문자 2개 곱셈 • 마플시너지 공통수학1 – 동류항 정리 심화💪 최종 정리
✅ 꼭 기억하세요!
- 곱셈 항 개수: 4개 × 3개 = 12개 항이 나옴
- 체계적 계산: 첫 번째 다항식의 각 항에 두 번째 다항식 전체를 곱함
- 핵심 주의: -y × (-y) = y² (음수 × 음수 = 양수!)
- 동류항 정리: xy항이 -2xy + (-2xy) = -4xy
- 정확도 우선: 빠르게 풀다가 실수하면 더 오래 걸림
- 목표 시간: 내신 3~4분, 수능 2.5~3.5분
🌟 선생님의 한마디
이 문제는 다항식 곱셈의 가장 기본입니다. 항이 많아서 복잡해 보이지만, 체계적으로 풀면 누구나 할 수 있어요!
특히 표를 그려서 곱셈하는 방법을 익히면 항을 빠뜨릴 걱정이 없습니다. 가로에 첫 번째 다항식, 세로에 두 번째 다항식을 쓰고, 교차하는 칸에 곱셈 결과를 쓰면 됩니다.
그리고 음수 × 음수 = 양수라는 규칙을 꼭 기억하세요! -y × (-y) = y²에서 많이 틀립니다. 이런 기본 곱셈을 정확하게 하는 연습이 나중에 인수분해에서 큰 도움이 됩니다! 💪
이 포스팅이 도움이 되셨다면 다른 문제 풀이도 확인해보세요!
궁금한 점은 댓글로 남겨주시면 친절하게 답변드리겠습니다. 😊