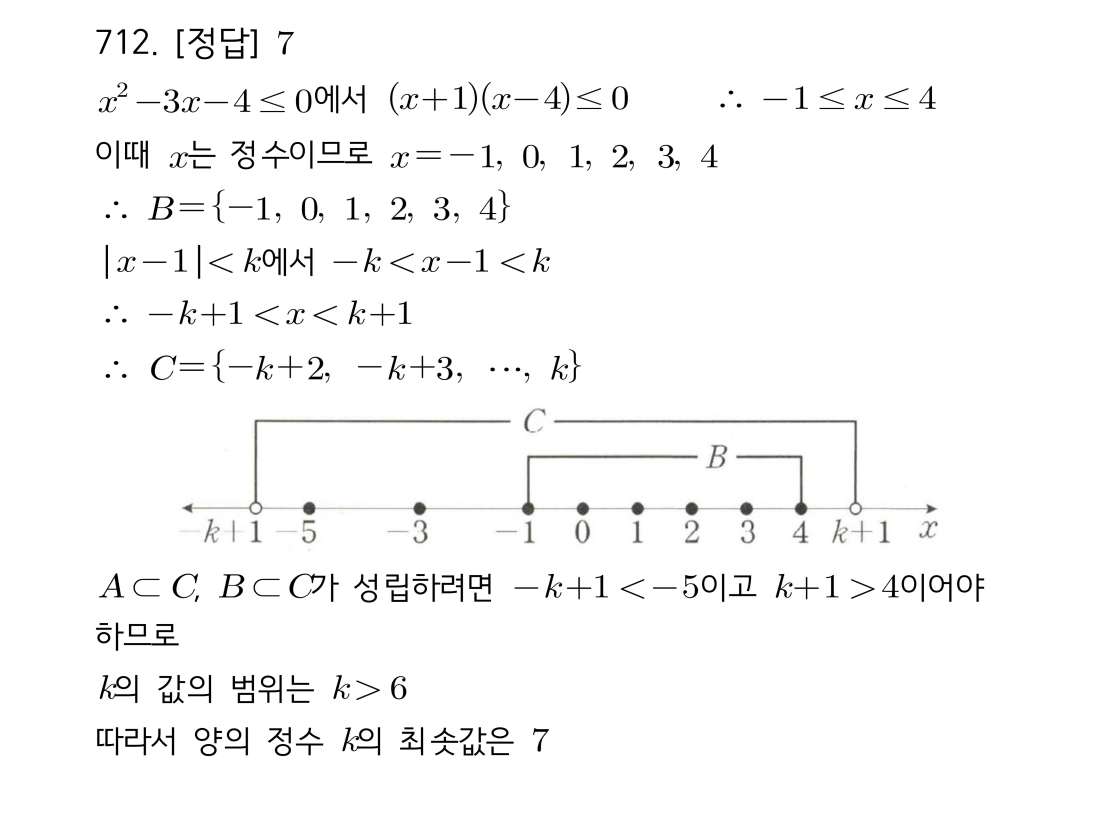
“

[문제 712] 핵심 개념 및 풀이 전략

두 집합이 모두 다른 한 집합의 부분집합이 될 조건을 이용해 미지수의 최솟값을 찾는 문제입니다.

접근법:
1. 세 집합 A, B, C를 모두 원소나열법 또는 범위로 나타냅니다.
– A = {-5, -3, -1, 1}
– B = {-1, 0, 1, 2, 3, 4}
– C = {정수 x | 1-k 2. **(A⊂C 조건)** 집합 C가 A의 모든 원소를 포함해야 합니다. A의 가장 작은 원소(-5)와 가장 큰 원소(1)를 기준으로 범위를 설정합니다. (1-k ≤ -5 그리고 1 3. **(B⊂C 조건)** 집합 C가 B의 모든 원소를 포함해야 합니다. B의 가장 작은 원소(-1)와 가장 큰 원소(4)를 기준으로 범위를 설정합니다. (1-k ≤ -1 그리고 4 4. 두 조건을 모두 만족하는 k의 공통 범위를 찾아, 양의 정수 k의 최솟값을 구합니다.

주의할 점:
C가 A와 B를 모두 포함하려면, A와 B를 합친 집합(A∪B)의 최소, 최대 원소를 모두 포함해야 합니다. 즉, C는 {-5, -3, -1, 0, 1, 2, 3, 4}를 포함해야 합니다.

”

두 집합을 모두 포함하는 집합의 조건