“

[문제 711] 핵심 개념 및 풀이 전략

연속적인 포함 관계(A⊂B⊂C)를 만족하는 미지수의 범위를 찾는 문제입니다.

접근법:
1. 세 집합 A, B, C를 각각 부등식의 해로 표현합니다.
– A = {x | -3 ≤ x ≤ 3}
– B = {x | -a – C = {x | -9 ≤ x ≤ 9}
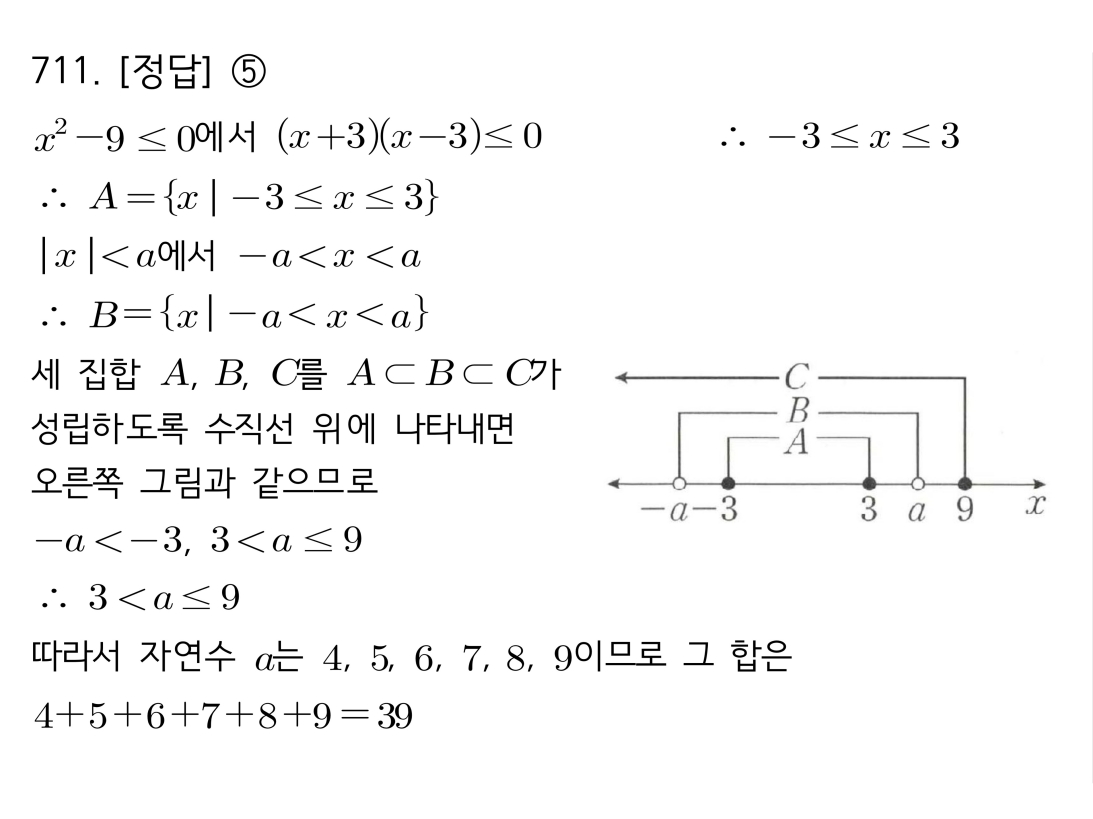
2. 수직선 위에 세 집합의 포함 관계가 나타나도록 그립니다.
3. (A⊂B 조건) -a 3.
4. (B⊂C 조건) -9 ≤ -a 이고 a ≤ 9 여야 합니다. 즉, a ≤ 9.
5. 두 조건을 모두 만족하는 자연수 a의 범위를 찾고, 그 합을 구합니다.

주의할 점:
각 포함 관계에 대해 부등식을 세우고, 최종적으로 연립부등식을 풀어 공통 범위를 찾아야 합니다.

”

세 집합의 연속적인 포함 관계(A⊂B⊂C)