마플시너지공통수학2풀이해설0631고퀄리티 풀이영상제공0631 기울어진 직선을 이용한 최단 거리

“

[문제 631] 핵심 개념 및 풀이 전략

대칭이동을 통해 최단 거리가 되는 점의 위치를 찾고, 그 점을 이용해 새로운 직선의 방정식을 구하는 문제입니다.

접근법:
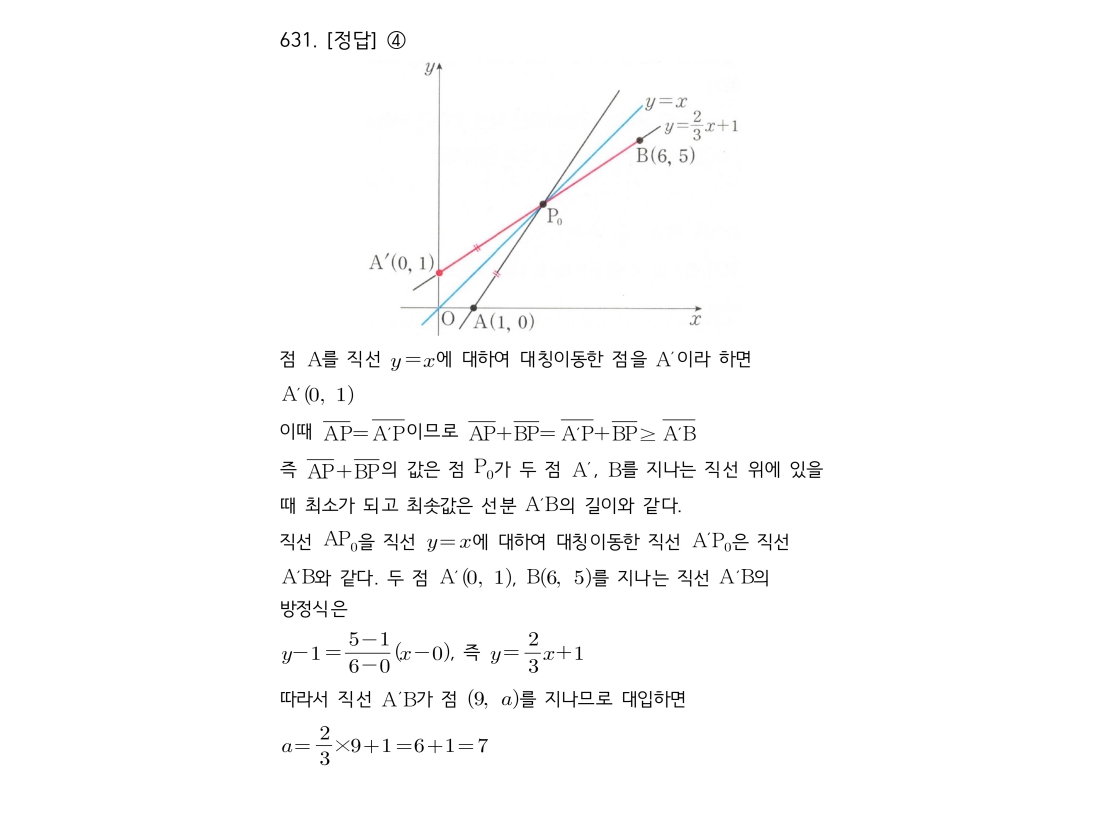
1. AP+BP가 최소가 되는 점 P₀는, 점 A(또는 B)를 y=x에 대해 대칭이동한 점과 나머지 점을 이은 직선과 y=x의 교점입니다.
2. 직선 AP₀를 y=x에 대해 대칭이동하면, 그 직선은 대칭점 A’과 B를 지나게 됩니다. 즉, **직선 A’B**가 됩니다.
3. 따라서, 두 점 A'(0,1)과 B(6,5)를 지나는 직선의 방정식을 구합니다.
4. 이 직선이 점 (9,a)를 지나므로, 좌표를 대입하여 a값을 구합니다.

주의할 점:
직선 AP₀의 대칭이동이 직선 A’B와 같아진다는 기하학적 관계를 이해하는 것이 중요합니다.

”

기울어진 직선을 이용한 최단 거리