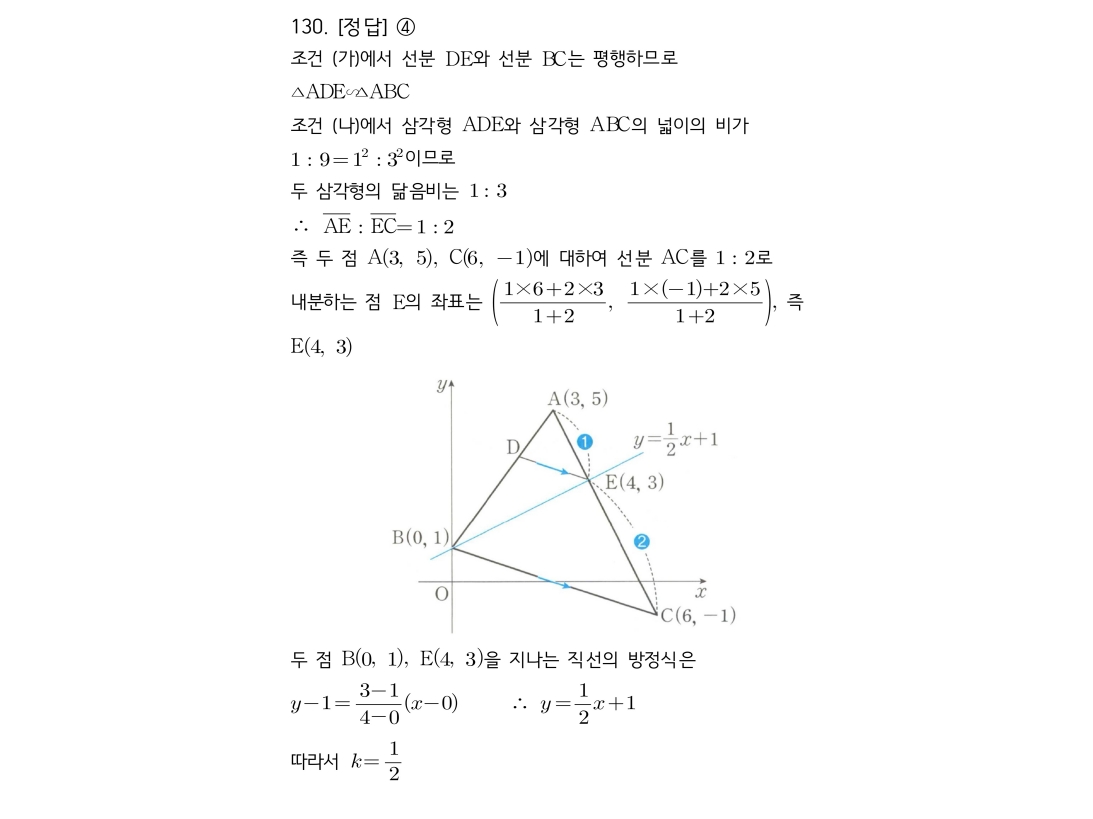
“

[문제 130] 핵심 개념 및 풀이 전략

삼각형의 닮음과 넓이 비의 관계를 이용해 선분의 내분점을 찾고, 이를 통해 직선의 방정식을 구하는 문제입니다.

접근법:
1. (가) 조건에서 선분 DE와 BC가 평행하므로, 삼각형 ADE와 ABC는 **닮음 관계**입니다.
2. (나) 조건에서 넓이의 비가 1:9 이므로, **닮음비(길이의 비)는 1:3** 입니다.
3. 따라서 AD:AB = AE:AC = 1:3 이며, 이는 점 E가 선분 AC를 **1:2로 내분하는 점**임을 의미합니다.
4. 내분점 공식을 이용해 점 E의 좌표를 구합니다.
5. 두 점 B와 E를 지나는 직선의 방정식을 구하여 기울기 k를 찾습니다.

주의할 점:
넓이의 비가 m:n 이면, 길이의 비(닮음비)는 √m : √n 이라는 점을 정확히 적용해야 합니다.

”

삼각형의 닮음과 넓이 비 활용