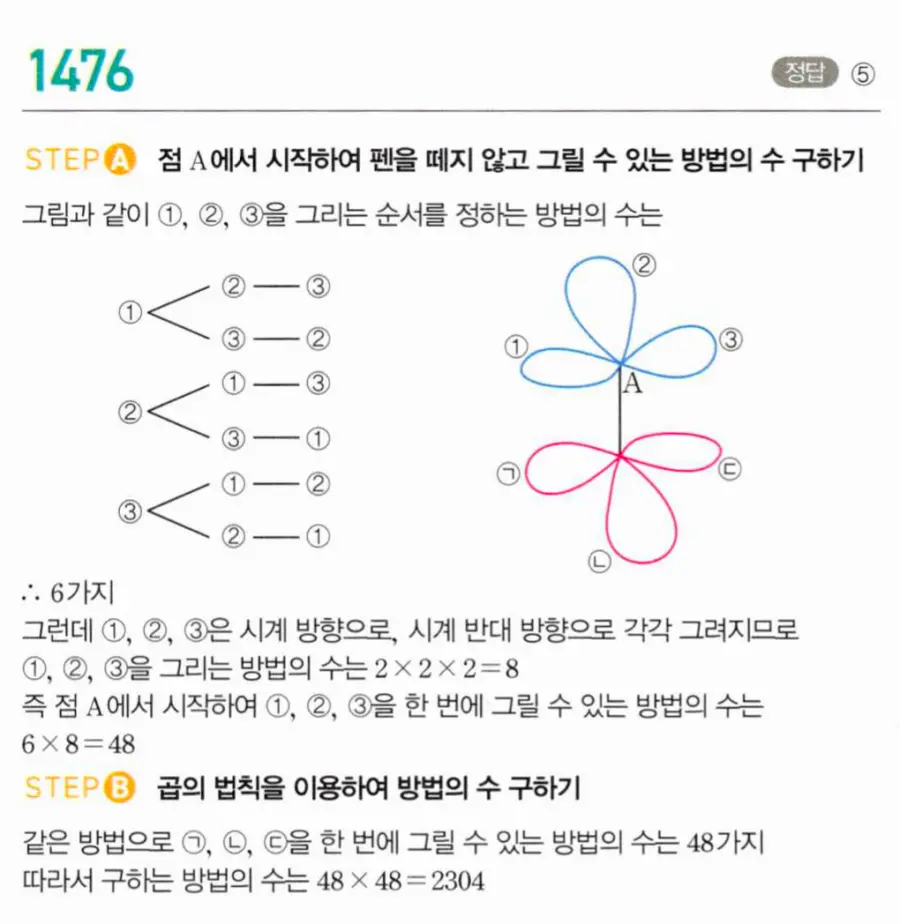
1485
최다빈출 · 홀짝 판정
정답 81
🔑 핵심 단서
홀짝 분석 abc + a + b + c가 홀수 → abc와 a+b+c의 홀짝이 달라야 함
범위 a, b, c는 각각 주사위 눈 {1~6} — 홀수 3개, 짝수 3개
핵심 abc의 홀짝과 a+b+c의 홀짝을 따로 판정한 뒤 조합
💡 왜 이렇게 풀어야 하는가
abc + (a+b+c)가 홀수 → 두 항의 홀짝이 달라야 합니다.
(i) abc 홀수, a+b+c 짝수:
abc 홀수 → a, b, c 모두 홀수
그런데 홀+홀+홀 = 홀 → a+b+c 짝수 불가능 → 0가지
(ii) abc 짝수, a+b+c 홀수:
a+b+c 홀수 → 홀수가 1개 또는 3개
3개 모두 홀수면 abc도 홀수 → 모순
∴ 홀수 1개, 짝수 2개
홀수가 놓이는 자리: 3가지 (a, b, c 중 택1)
각 배치: 3 × 3 × 3 = 27가지
총: 27 × 3 = 81
① 홀짝 조건 분석
② (i) 불가능 확인
③ (ii) 홀1·짝2
④ 배치 × 선택지
📺 해설 강의
📝 해설 이미지
클릭하면 원본 크기로 열립니다
⚠️ 자주 하는 실수
(i)이 가능하다고 착각 — 세 수 모두 홀수이면 합도 반드시 홀수이므로 불가
홀수 3개를 (ii)에 포함 — abc가 홀수가 되어 조건 위반
배치 3가지를 빠뜨림 — (홀,짝,짝), (짝,홀,짝), (짝,짝,홀) 모두 고려
전체 216에서 빼려다 계산 실수 — 직접 세기가 더 안전
27 × 3 = 81