마플시너지 공통수학1 1209번 행복한 1등급 – 8단원 부등식, |x−a| < 2를 만족시키는 모든 실수 x가 |x−6| ≥ a를 만족시킬 때 양수 a의 최댓값
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 8단원 · 부등식과 방정식 |
| 🔢 문제번호 | 1209번 |
| 📋 유형 | 절댓값 부등식 · 해의 포함관계 |
| ⭐ 난이도 | 행복한 1등급 + 최다빈출 왕중요 |
마플시너지공수1답지 1209번 행복한 1등급 절댓값 포함관계 핵심 포인트
1209번은 8단원 부등식 행복한 1등급 + 최다빈출 왕중요 문제로, |x−a| < 2를 만족시키는 모든 실수 x가 부등식 |x−6| ≥ a를 만족시킬 때 양수 a의 최댓값을 구하는 문제입니다.
STEP A. 각각의 절댓값 부등식의 해 구하기
|x−a| < 2에서 −2 < x−a < 2, a−2 < x < a+2 ···㉮. |x−6| ≥ a에서 a > 0이므로 x−6 ≤ −a 또는 x−6 ≥ a, 즉 x ≤ −a+6 또는 x ≥ a+6 ···㉯.
STEP B. 두 부등식의 해의 포함관계를 이용하여 양수 a의 최댓값 구하기
|x−a| < 2를 만족시키는 모든 실수 x가 |x−6| ≥ a를 만족시키려면 ㉮가 ㉯의 해에 포함되어야 합니다. ㉯는 x ≤ −a+6 또는 x ≥ a+6이고, ㉮는 a−2 < x < a+2인 연속 구간입니다.
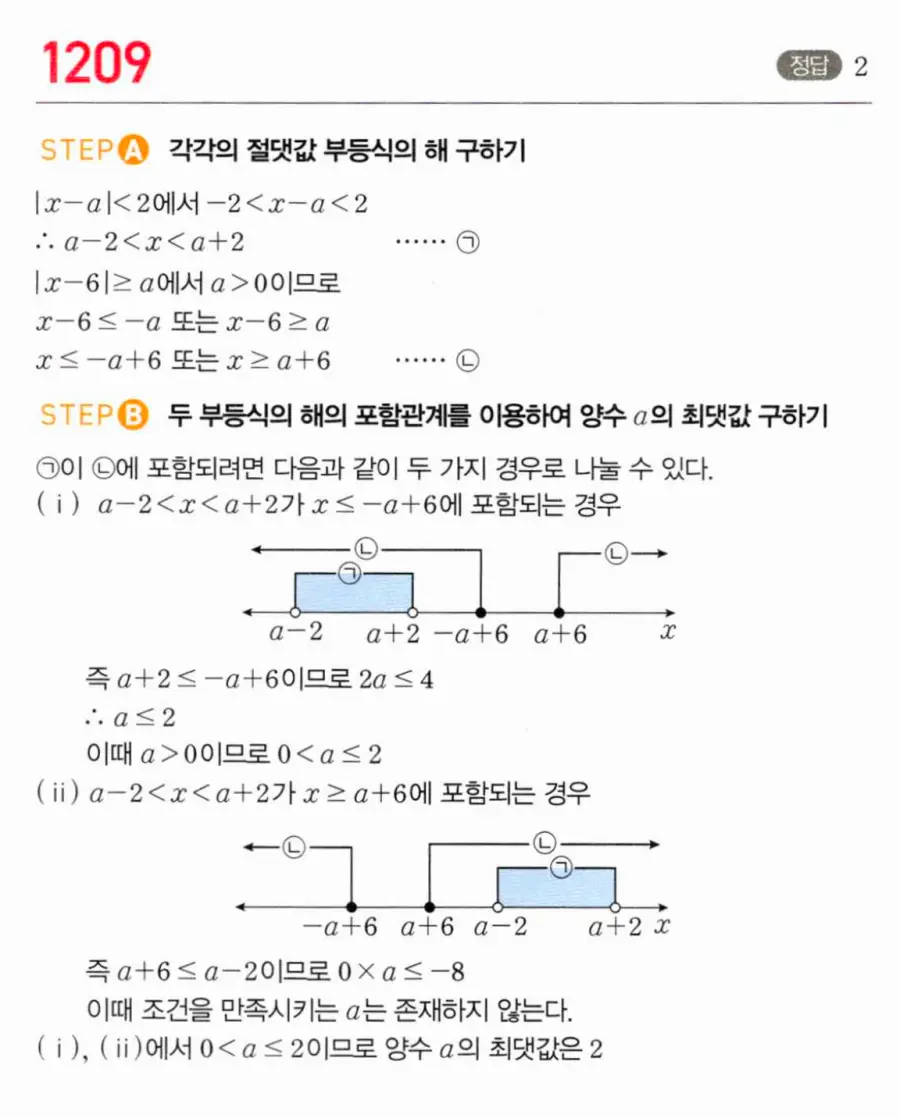
㉮가 ㉯에 포함되려면 다음과 같이 두 가지 경우로 나눌 수 있습니다.
(ⅰ) a−2 < x < a+2가 x ≤ −a+6에 포함되는 경우: a+2 ≤ −a+6이므로 2a ≤ 4, a ≤ 2. 이때 a > 0이므로 0 < a ≤ 2.
(ⅱ) a−2 < x < a+2가 x ≥ a+6에 포함되는 경우: a−2 ≥ a+6이므로 −2 ≥ 6. 모순이므로 이 경우는 존재하지 않습니다.
(ⅰ), (ⅱ)에서 0 < a ≤ 2이므로 양수 a의 최댓값은 2.
1209번 행복한 1등급 엄선 풀이영상
▲ 8단원 부등식 행복한 1등급 · |x−a|<2 ⊂ |x−6|≥a → a+2≤−a+6 → a≤2 → 최댓값 2 1209번 전 과정 해설
1209번 답지 확인