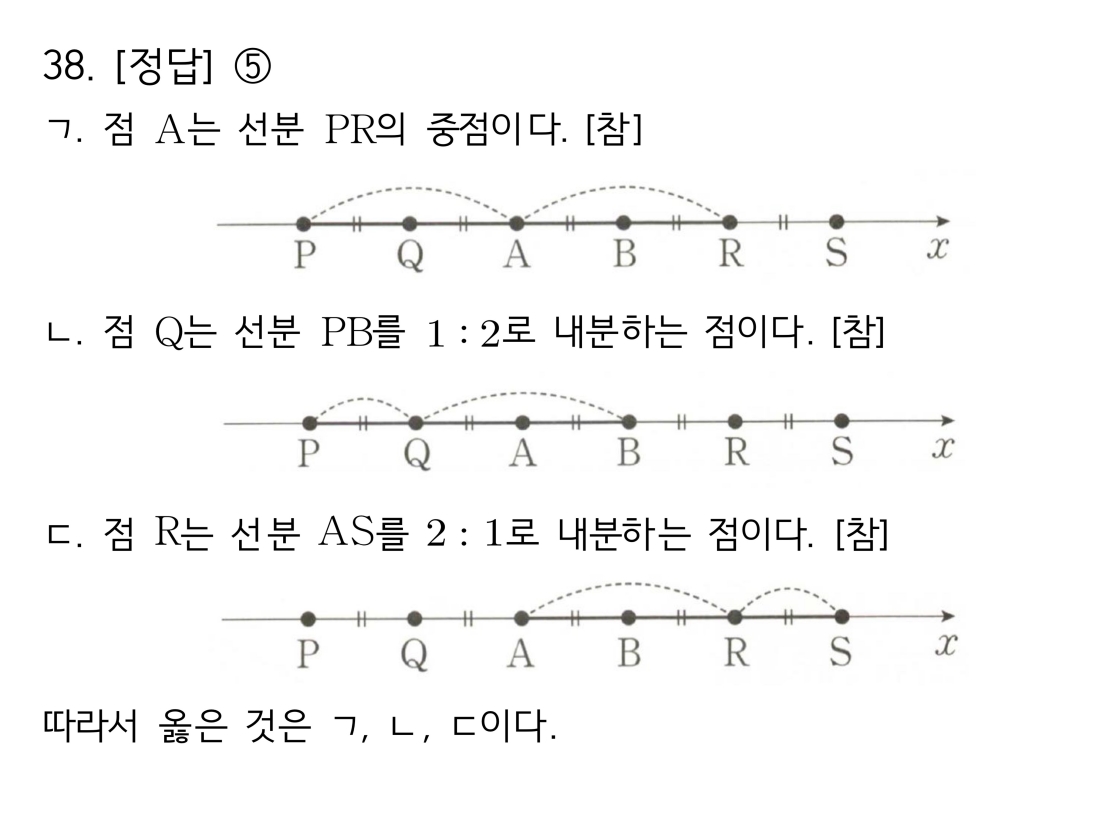
마플시너지공통수학2풀이해설0039고퀄리티 풀이영상제공0039 수직선 위 내분점/중점 좌표 계산
“ [문제 39] 핵심 개념 및 풀이 전략 여러 개의 조건을 종합하여 수직선 위에 표현되지 않은 점들의 위치를 추론하고 길이를 구하는 문제입니다. 접근법:1. 주어진 점 B(1), D(5)를 기준으로 나머지 점들의 좌표를 순서대로 찾습니다.2. (나) 조건에서 점 C는 선분 AD를 2:1로 내분하므로, C의 좌표를 이용해 A의 좌표를 찾을 수 있습니다.3. (가) 조건에서 점 B는 선분 AC의 … 더 읽기