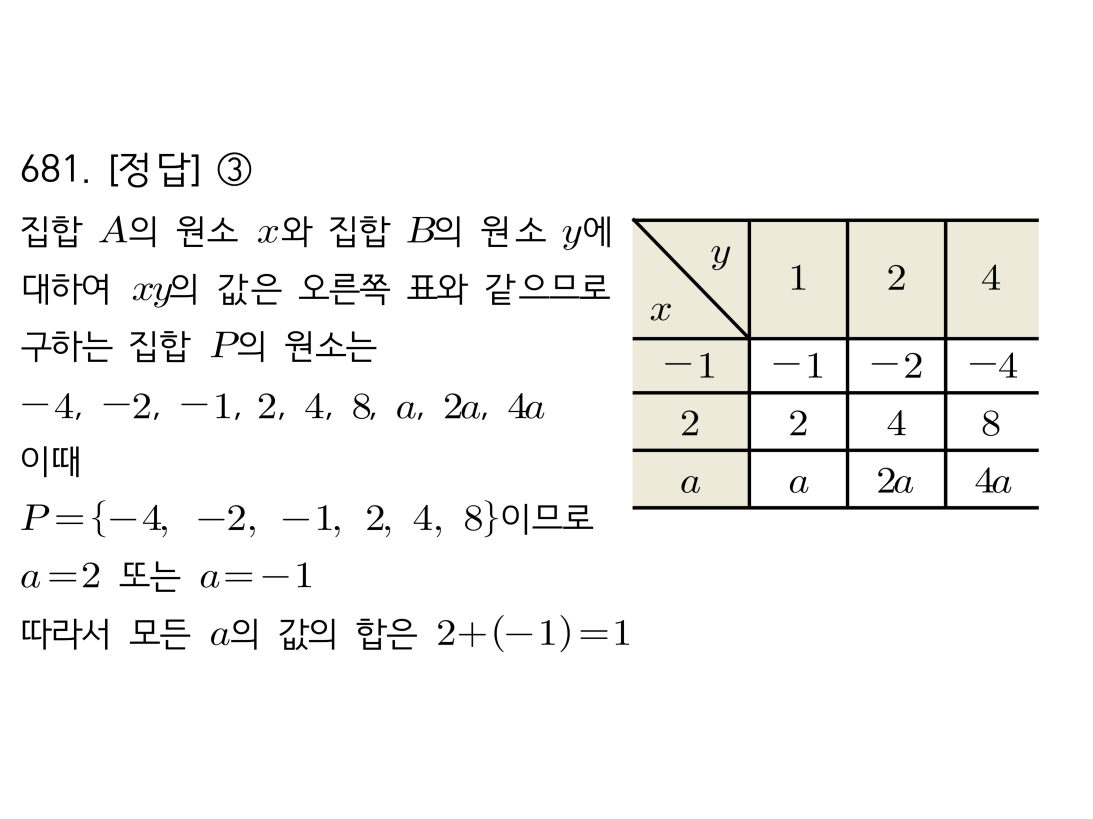
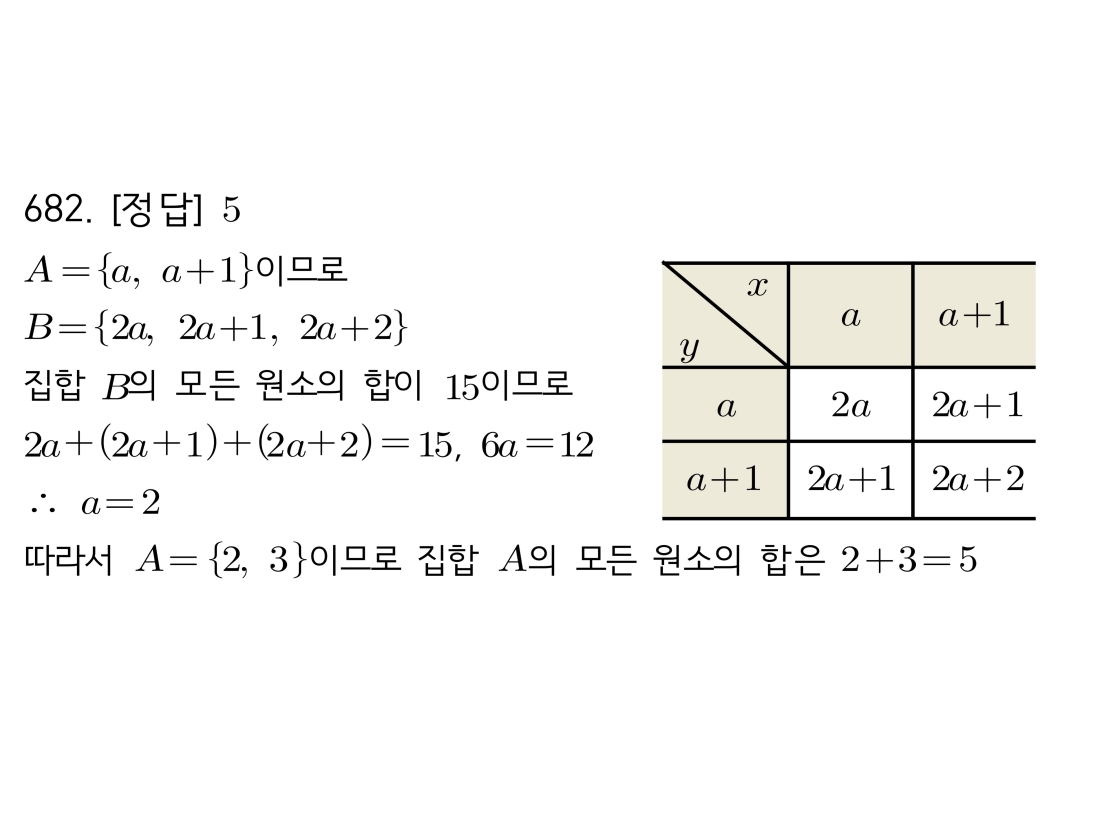
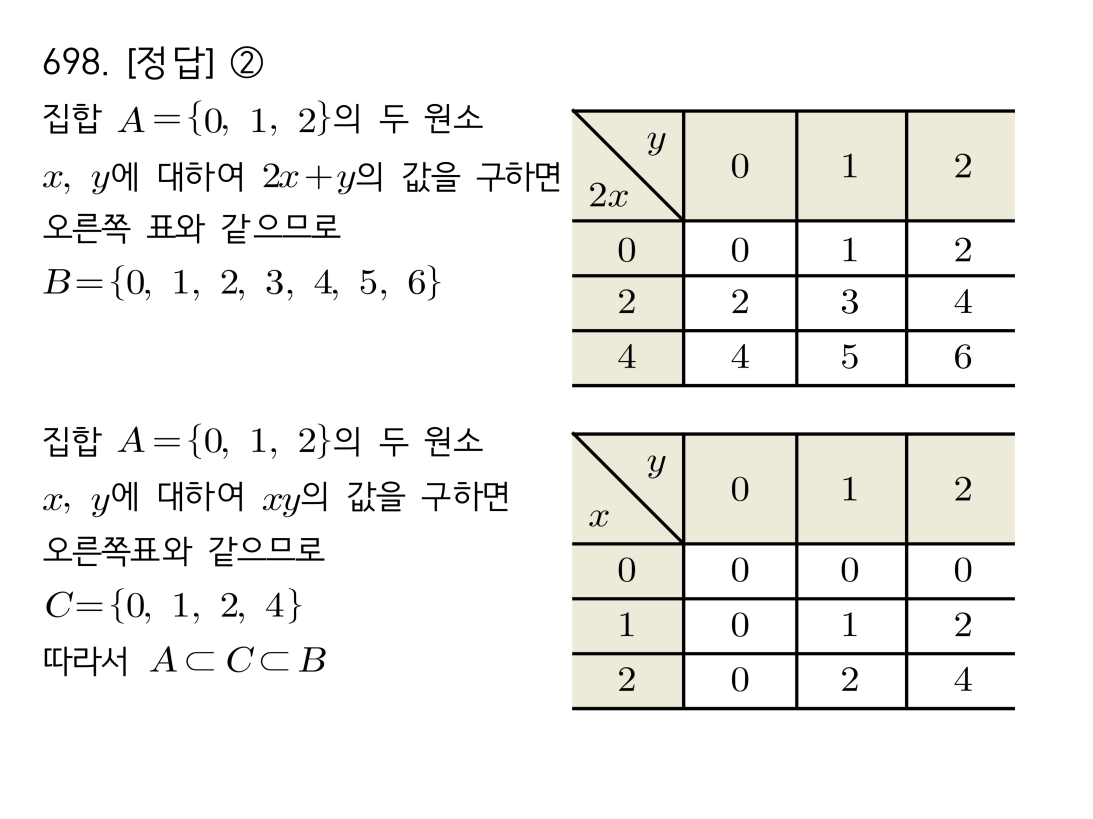
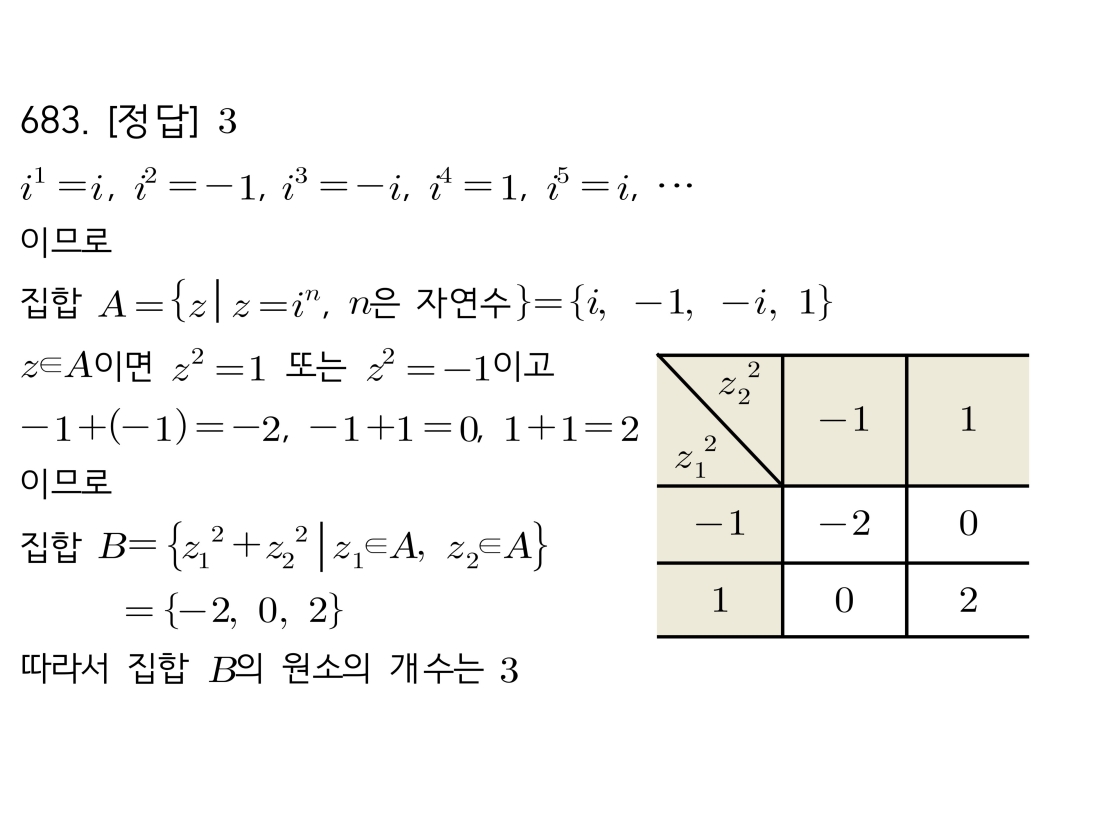
마플시너지공통수학2풀이해설0692고퀄리티 풀이영상제공0692 이차부등식의 해가 없는 집합(공집합)
“ [문제 692] 핵심 개념 및 풀이 전략 이차부등식의 해를 원소로 하는 집합이 공집합이 될 조건을 이용하는 문제입니다. 접근법:1. 집합 A가 공집합(A=∅)이 되려면, 부등식 x²-2kx+2k+8 < 0을 만족하는 **실수 x가 존재하지 않아야** 합니다.2. 이는 모든 실수 x에 대하여 부등식 **x²-2kx+2k+8 ≥ 0** 이 항상 성립해야 함을 의미합니다.3. 아래로 볼록한 이차함수가 항상 0 이상이려면, x축에 접하거나(중근) ... 더 읽기