0083번 – 나눗셈 등식 A = BQ + R
나누는 다항식 구하기
피제식, 몫, 나머지가 주어졌을 때 나누는 식 A 역추적!
이 포스팅에 포함된 것들
- 풀이 영상 (유튜브)
- 해설 이미지 (쎈 답지)
- 문제 분석 & 핵심 단서 찾기
- 단계별 상세 풀이
- 자주 틀리는 실수 & 꿀팁
- 외워두면 좋은 패턴 정리
- 시간 관리 전략
- 관련 개념·연산·마플시너지 링크
🎬 풀이 영상
영상으로 먼저 풀이 흐름을 파악해 보세요!
🔍 문제 분석
[문제 요약]
다항식 x⁴ − 3x² + x − 5 를 다항식 A로 나누었을 때의
몫이 x² − x + 3 이고, 나머지가 −7x + 10 일 때, 다항식 A는?
① x²−x−3 ② x²−x+2 ③ x²+x−5 ④ x²+x−3 ⑤ x²+2x−4
※ 난이도: ★★☆ (중) · 대표 문제 · 답: ③ x²+x−5
이 문제의 핵심을 짚어볼게요!
① 피제식(나눠지는 식), 몫, 나머지가 모두 주어져 있어요!
② 대신 나누는 식 A를 구해야 합니다 → 나눗셈 등식을 역으로 사용!
③ 나눗셈 등식: (피제식) = A × (몫) + (나머지)
④ A를 구하려면: A = (피제식 − 나머지) ÷ (몫)
💡 핵심: 나눗셈 등식을 변형하여 A에 대해 정리!
이 문제는 유형 10의 대표 문제로, 나눗셈 등식 A = BQ + R에서 미지의 부분을 역추적하는 문제예요. 기존에는 Q(몫)나 R(나머지)를 구했다면, 이번에는 B(나누는 식)를 구하는 역방향 사고가 필요합니다!
📝 단계별 상세 풀이
나눗셈 등식 세우기
(피제식) = A × (몫) + (나머지)
x⁴ − 3x² + x − 5 = A · (x² − x + 3) + (−7x + 10)
A에 대해 정리하기
A · (x² − x + 3) = (x⁴ − 3x² + x − 5) − (−7x + 10)
= x⁴ − 3x² + x − 5 + 7x − 10
= x⁴ − 3x² + 8x − 15
따라서:
A = (x⁴ − 3x² + 8x − 15) ÷ (x² − x + 3)
💡 나머지를 빼면 “나누어떨어지는 식”이 돼요! 이제 나눗셈만 하면 됩니다.
나눗셈 실행하기
x⁴ + 0x³ − 3x² + 8x − 15 를 x² − x + 3 으로 나눕니다.
① x⁴ ÷ x² = x²
x²(x²−x+3) = x⁴−x³+3x²
빼기: (x⁴−3x²+8x−15)−(x⁴−x³+3x²) = x³−6x²+8x−15
② x³ ÷ x² = x
x(x²−x+3) = x³−x²+3x
빼기: (x³−6x²+8x−15)−(x³−x²+3x) = −5x²+5x−15
③ −5x² ÷ x² = −5
−5(x²−x+3) = −5x²+5x−15
빼기: (−5x²+5x−15)−(−5x²+5x−15) = 0
💡 나머지가 0! 깔끔하게 나누어떨어져요. (당연히 그래야 합니다!)
결과 확인
A = x² + x − 5
⚠️ 자주 틀리는 실수
나머지를 빼는 과정에서 부호 실수!
(x⁴−3x²+x−5) − (−7x+10)
= x⁴−3x²+x−5+7x−10 ✅ (부호 전체 반전!)
= x⁴−3x²+x−5−7x+10 ❌
→ −(−7x+10) = +7x−10 이에요! 빼기의 빼기는 더하기!
빠진 x³ 항을 잊는 실수!
x⁴−3x²+8x−15 에는 x³항이 없어요! (계수 0)
나눗셈할 때 x⁴+0x³−3x²+8x−15 으로 써야 해요.
나눗셈 방향을 혼동하는 실수!
A = (피제식−나머지) ÷ (몫) ✅
A = (피제식−나머지) ÷ (나머지) ❌
→ 몫으로 나누는 거예요! 등식을 차분히 정리하면 헷갈리지 않아요.
🧠 외워두면 좋은 패턴
이 등식에서 어떤 것이든 미지수가 될 수 있어요!
• 제식(나누는 식) 구하기: 제식 = (피제식 − 나머지) ÷ 몫
• 피제식 구하기: 피제식 = 제식 × 몫 + 나머지
• 몫 구하기: 직접 나눗셈 실행
• 나머지 구하기: 나머지 = 피제식 − 제식 × 몫
나누는 식을 구할 때의 풀이 순서:
1단계: 피제식에서 나머지를 빼기 → 나누어떨어지는 식 만들기
2단계: 그 식을 몫으로 나누기 → 나누는 식 = 결과
→ 나머지를 빼면 “깔끔하게 나누어떨어지는” 상태가 돼요!
피제식(4차) = 제식(?) × 몫(2차) + 나머지(1차)
→ 제식의 차수 = 4 − 2 = 2차
→ 보기가 모두 2차식이므로 차수 조건은 맞아요. 추가 검산에 활용!
⏱️ 시간 관리 전략
| 시험 유형 | 처음 풀 때 | 익숙해진 후 | 목표 시간 |
|---|---|---|---|
| 내신 시험 | 5~6분 | 2~3분 | 2분 30초 |
| 수능/모의고사 | 4~5분 | 2분 | 2분 |
① 등식 변형을 머릿속에서 바로!
“제식 구하기 = (피제식−나머지)÷몫” 이 공식을 외워두면 방향 잡는 시간이 0초!
② 보기를 활용한 검산도 가능!
시간이 부족하면 보기 중 하나를 넣어서 검산할 수도 있어요. A×(몫)+(나머지)=(피제식) 인지 확인!
③ 빠진 항(0x³)을 미리 표시!
나눗셈 시작 전에 빠진 차수를 0으로 채워 두면 실수가 크게 줄어요.
📸 해설 이미지
교재 해설을 이미지로 확인하세요.
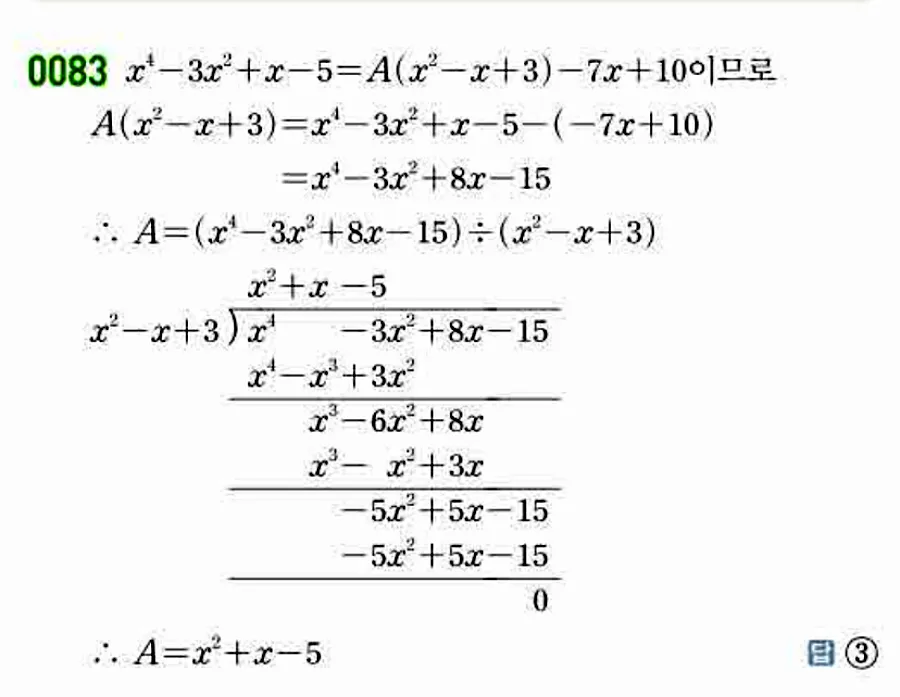
📚 추천 학습 순서
1단계: 연산 워크시트나눗셈 연산력을 키우세요!
공통수학1 연산 10. 나머지 정리 ⭐ 공통수학1 연산 12. 조립제법 공통수학1 연산 11. 인수 정리 공통수학1 연산 03. 다항식의 곱셈 (1) 공통수학1 연산 02. 다항식의 덧셈과 뺄셈개념을 확실히 잡고 가세요!
개념사전 012. 다항식 나눗셈과 등식 ⭐ (이 문제의 핵심!) 개념사전 011. 다항식÷다항식 계산 개념사전 016. 나머지정리 이해 개념사전 018. 조립제법 계산 개념사전 010. 다항식÷단항식 계산유사 문제로 실력을 굳히세요!
마플시너지 공수1 – 01-4. 다항식의 나눗셈 ⭐ 마플시너지 공수1 – 01-3. 곱셈 공식의 변형 마플시너지 공수1 – 01-2. 곱셈 공식을 이용한 전개