0071번 – 곱셈 공식의 변형
a²+b²+c², 1/a+1/b+1/c 값 구하기
세 수의 합·제곱합·곱 조건에서 역수의 합 구하기
이 포스팅에 포함된 것들
- 풀이 영상 (유튜브)
- 해설 이미지 (쎈 답지)
- 문제 분석 & 핵심 단서 찾기
- 단계별 상세 풀이
- 자주 틀리는 실수 & 꿀팁
- 외워두면 좋은 패턴 정리
- 시간 관리 전략
- 관련 개념·연산·마플시너지 링크
🎬 풀이 영상
영상으로 먼저 풀이 흐름을 파악해 보세요!
🔍 문제 분석
[문제 요약]
세 수 a, b, c에 대해 다음 세 조건이 주어져 있을 때:
a + b + c = 3, a² + b² + c² = 15, abc = −1
1/a + 1/b + 1/c 의 값은?
※ 난이도: ★★☆ (중) · 대표 문제 · 답: ③ 3
이 문제에서 꼭 잡아야 할 단서 3가지!
① 세 조건이 모두 대칭식 → a+b+c, a²+b²+c², abc가 주어졌으므로 ab+bc+ca를 구하면 모든 대칭식을 처리할 수 있어요.
② 1/a + 1/b + 1/c는 통분하면 (ab+bc+ca) / abc로 변환돼요!
③ (a+b+c)² = a²+b²+c² + 2(ab+bc+ca) 공식으로 ab+bc+ca를 바로 구할 수 있어요.
이 문제는 유형 07 (곱셈 공식의 변형)의 대표 문제입니다. “세 수의 합, 제곱합, 곱”이 동시에 주어지면, ab+bc+ca를 먼저 구하는 것이 핵심 전략이에요. 한번 익혀두면 같은 유형을 1분 안에 풀 수 있습니다!
📝 단계별 상세 풀이
ab + bc + ca 구하기
핵심 공식: (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
양변에 값을 대입하면:
3² = 15 + 2(ab + bc + ca)
9 = 15 + 2(ab + bc + ca)
2(ab + bc + ca) = 9 − 15 = −6
∴ ab + bc + ca = −3
💡 이 한 단계가 이 문제의 핵심이에요! (a+b+c)²을 전개하는 공식 하나로 끝!
1/a + 1/b + 1/c 를 통분하여 변환하기
1/a + 1/b + 1/c = (bc + ac + ab) / abc
→ 통분하면 분자에는 ab+bc+ca가, 분모에는 abc가 들어갑니다!
값 대입하여 계산하기
1/a + 1/b + 1/c = (ab + bc + ca) / abc
= (−3) / (−1)
= 3
⚠️ 자주 틀리는 실수
(a+b+c)² 전개 공식을 잘못 쓰는 경우!
(a+b+c)² = a²+b²+c² + 2(ab+bc+ca) ✅
(a+b+c)² = a²+b²+c² + ab+bc+ca ❌ (2가 빠짐!)
1/a + 1/b + 1/c 통분 실수!
분자가 ab + bc + ca 인데, a+b+c로 잘못 쓰는 학생이 있어요.
→ 직접 통분해 보면: 1/a + 1/b + 1/c = (bc + ac + ab) / (abc) 입니다!
부호 실수!
abc = −1 이므로 (−3)÷(−1) = 3 (양수)입니다.
→ 음수÷음수 = 양수! 부호를 꼼꼼히 확인하세요.
🧠 외워두면 좋은 패턴
세 수 a, b, c에 대한 모든 대칭식은 다음 3개로 표현됩니다:
① a + b + c ② ab + bc + ca ③ abc
→ 이 세 값만 알면 어떤 대칭식이든 구할 수 있어요!
(a+b+c)² = a²+b²+c² + 2(ab+bc+ca)
→ ab+bc+ca = {(a+b+c)² − (a²+b²+c²)} / 2
→ “합의 제곱에서 제곱의 합을 빼고 2로 나누면 짝지어 곱한 합”
1/a + 1/b + 1/c = (ab + bc + ca) / abc
1/a² + 1/b² + 1/c² = (a²b² + b²c² + c²a²) / (abc)²
→ 역수의 합은 항상 통분해서 대칭식으로 바꾸는 것이 정석!
⏱️ 시간 관리 전략
| 시험 유형 | 처음 풀 때 | 익숙해진 후 | 목표 시간 |
|---|---|---|---|
| 내신 시험 | 3~4분 | 1~2분 | 1분 30초 |
| 수능/모의고사 | 2~3분 | 1분 | 1분 |
① “세 조건 = 세 대칭식” 패턴을 인식하세요!
a+b+c, a²+b²+c², abc가 보이는 순간 “ab+bc+ca부터 구한다”는 경로가 자동으로 떠올라야 해요.
② 역수의 합 → 통분은 반사적으로!
1/a + 1/b + 1/c = (ab+bc+ca)/abc 이 공식은 외워서 바로 쓸 수 있도록 연습하세요.
③ 계산 순서를 정해놓으세요!
이 유형은 항상 (a+b+c)² 전개 → ab+bc+ca 구하기 → 원하는 식에 대입 순서로 풀면 됩니다.
📸 해설 이미지
교재 해설을 이미지로 확인하세요.
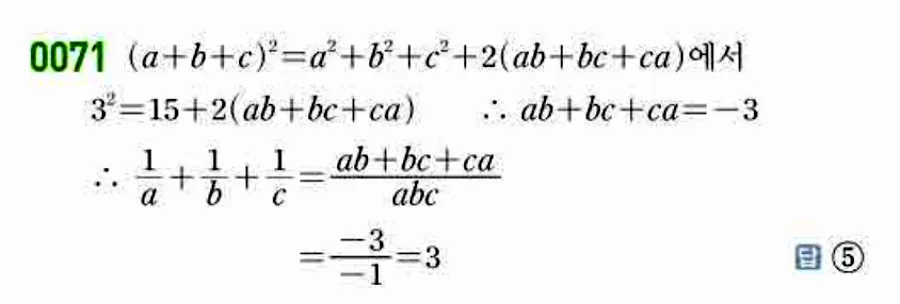
📚 추천 학습 순서
1단계: 연산 워크시트기본 연산력부터 탄탄하게!
공통수학1 연산 07. 곱셈 공식의 변형 ⭐ (이 문제와 직접 관련!) 공통수학1 연산 05. 곱셈 공식 (1) 공통수학1 연산 06. 곱셈 공식 (2) 공통수학1 연산 03. 다항식의 곱셈 (1) 공통수학1 연산 04. 다항식의 곱셈 (2) 공통수학1 연산 02. 다항식의 덧셈과 뺄셈개념을 확실히 잡고 가세요!
개념사전 009. 곱셈공식의 변형 활용 ⭐ (필수) 개념사전 008. 곱셈공식 정리 개념사전 006. 식 전개하기 개념사전 007. 다항식 곱셈의 연산법칙 개념사전 005. 지수의 법칙 개념사전 001. 다항식의 기본 용어유사 문제로 실력을 굳히세요!
마플시너지 공수1 – 01-3. 곱셈 공식의 변형 ⭐ 마플시너지 공수1 – 01-2. 곱셈 공식을 이용한 전개 마플시너지 공수1 – 01-1. 다항식의 덧셈과 뺄셈