1441
2017년 06월 고1 학력평가 21번
정답 ① 3/2
🔑 핵심 단서
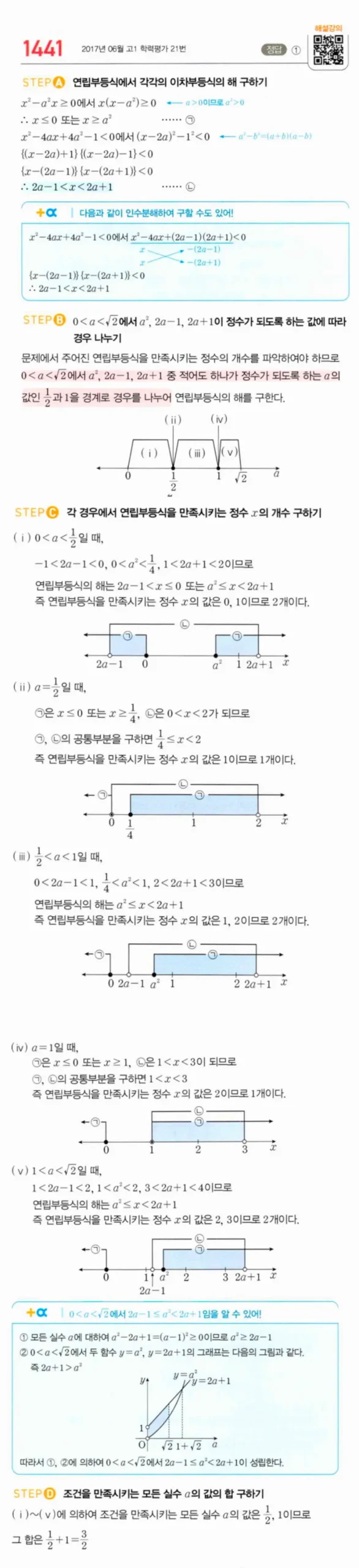
인수분해 첫째 식: x(x − a²) ≥ 0 → x ≤ 0 또는 x ≥ a²
완전제곱 둘째 식: (x − 2a)² < 1 → 2a−1 < x < 2a+1 (폭 = 2)
경계값 0 < a < √2에서 a², 2a−1, 2a+1의 대소가 바뀌는 a = 1/2, 1이 분류 기준
💡 왜 이렇게 풀어야 하는가
ⓐ은 “x ≤ 0 또는 x ≥ a²”로 양 끝, ⓛ은 길이 2 구간. 교집합에 정수가 딱 1개인 a를 찾아야 합니다.
핵심: 2a−1 ≤ a²이 항상 성립 (∵ (a−1)² ≥ 0). 그래서 공통구간은 a² ≤ x < 2a+1 부분만 보면 됩니다.
a가 변하면 이 구간에 들어가는 정수 수가 달라지므로, 경계점에서 정확히 1개가 되는 a를 찾습니다.
① 각 부등식 해
② 경계값 (1/2, 1)
③ 구간별 정수 세기
④ 합산
0 < a < 1/2
정수 0, 1 → 2개a = 1/2
정수 1만 → 1개 ✓1/2 < a < 1
정수 1, 2 → 2개a = 1
정수 2만 → 1개 ✓1 < a < √2
정수 1~2개 변동∴ a = 1/2 + 1 = 3/2
⚠️ 자주 하는 실수
둘째 식을 완전제곱으로 못 바꿈 — (x−2a)²−1 < 0으로 보면 해가 바로 나옴
경우 분류 없이 대략 판단 — 경계점 a = 1/2, 1에서만 정확히 1개
ⓐ의 해를 “0 ≤ x ≤ a²”로 오독 — 실제는 x ≤ 0 또는 x ≥ a² (두 조각)
2a−1 ≤ a² 관계를 확인 안 함 — (a−1)² ≥ 0이 근거
a = 1/2일 때 x = 0이 ⓛ에 포함된다고 착각 — 열린 부등호이므로 미포함
a = 1/2 + 1 = 3/2