🔥 TOUGH
📋 2020년 9월 고1 학평 14번
마플시너지 공통수학1 1227번 TOUGH – 9단원 이차부등식, f(x) = a(x−2)(x−b)에서 조건 (가) f(0) = 6, 조건 (나) x > 2일 때 f(x) > 0일 때 f(4)
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 9단원 · 이차부등식 |
| 🔢 문제번호 | 1227번 |
| 📋 출처 | 2020년 09월 고1 학력평가 14번 |
| ⭐ 난이도 | TOUGH |
마플시너지공수1답지 1227번 TOUGH 이차함수 조건 결정 핵심 포인트
1227번은 9단원 이차부등식 TOUGH 문제(2020년 9월 고1 학평 14번)로, 두 자연수 a, b에 대하여 이차함수 f(x) = a(x−2)(x−b)가 (가) f(0) = 6, (나) x > 2일 때 f(x) > 0을 만족시킬 때 f(4)를 구하는 문제입니다.
STEP A. 조건 (가)를 만족시키는 자연수 a, b의 값 구하기
f(0) = a(0−2)(0−b) = 2ab = 6이므로 ab = 3. a, b가 자연수이므로 a = 1, b = 3 또는 a = 3, b = 1.
STEP B. 조건 (나)를 만족하는 자연수 a, b의 값 구하기
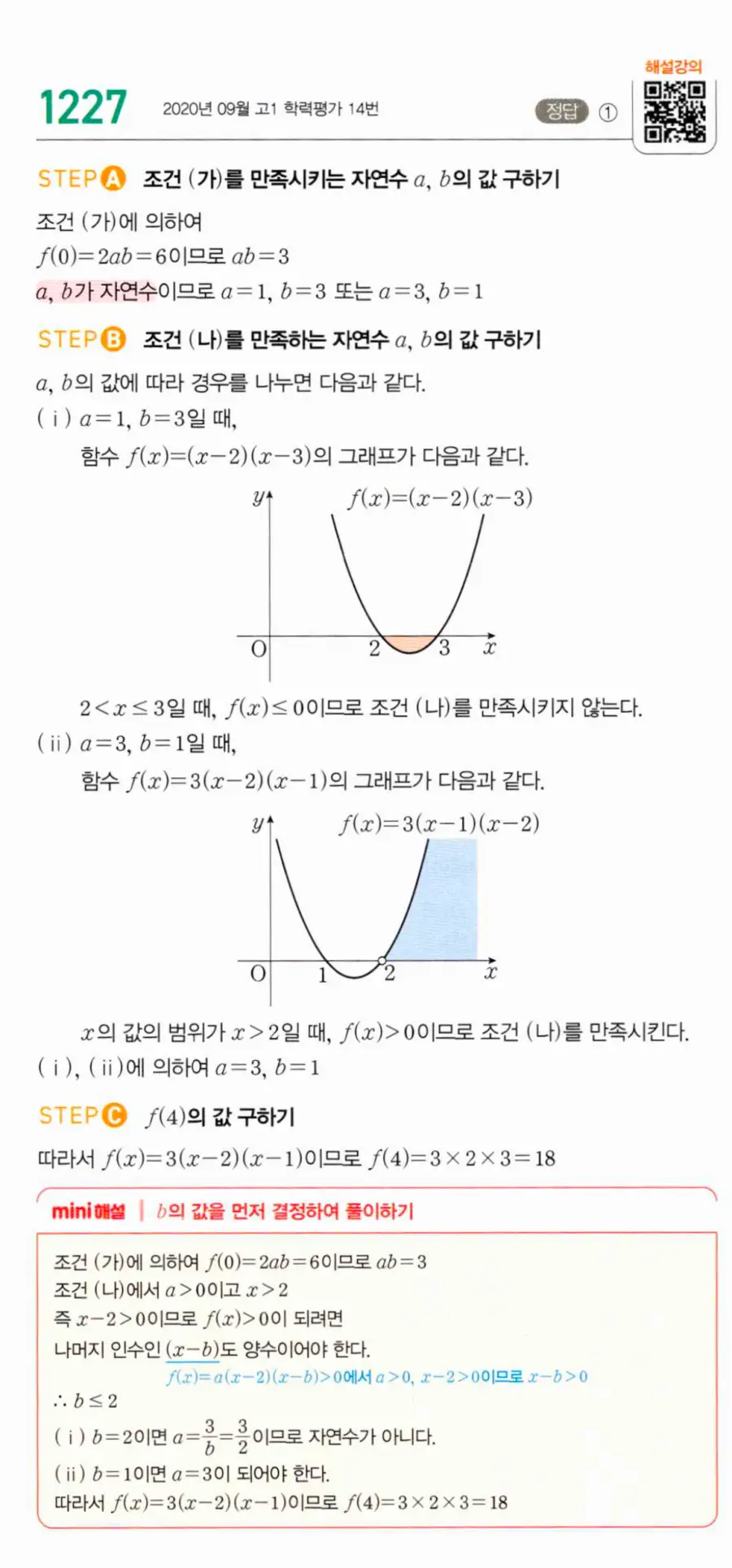
(ⅰ) a = 1, b = 3일 때: f(x) = (x−2)(x−3). x > 2일 때, 2 < x ≤ 3에서 f(x) ≤ 0이므로 조건 (나)를 만족시키지 않습니다.
(ⅱ) a = 3, b = 1일 때: f(x) = 3(x−2)(x−1). x > 2이면 x−2 > 0이고 x−1 > 0이므로 f(x) > 0. 조건 (나)를 만족시킵니다.
따라서 a = 3, b = 1.
STEP C. f(4)의 값 구하기
f(x) = 3(x−2)(x−1)이므로 f(4) = 3×(4−2)×(4−1) = 3×2×3 = 18.
정답: ① 18
1227번 TOUGH 엄선 풀이영상
▲ 9단원 이차부등식 TOUGH · f(x)=3(x−2)(x−1) → f(4)=18 1227번 전 과정 해설
1227번 답지 확인