라이트쎈 확률과 통계 07. 통계적 추정 답지
🔥 **필독!** 이 페이지는 **단순 답지**를 넘어 **20년 경력 강사가 엄선한 문제 풀이 영상과 이론 정리 영상**이 포함된 학습 가이드 포스팅입니다. 해설지보다 더 명쾌한 풀이를 경험하세요.
수고하셨습니다! **라이트쎈 확률과 통계** **07단원 통계적 추정** 마지막 단원입니다.
**통계적 추정**은 표본을 통해 모집단의 특성을 추론하는 개념입니다. **표본 평균의 분포**와 **모평균의 신뢰구간** 공식을 정확히 외우는 것이 중요하며, **표준화** 과정을 통해 확률을 계산합니다.
[Image of confidence interval formula for population mean]
📌 학습 팁: 표본평균 $\mathbf{\bar{X}}$의 분산
표본평균의 분산($V(\bar{X})$)은 모분산($\sigma^2$)을 표본의 크기($n$)로 나눈 $\mathbf{\frac{\sigma^2}{n}}$ 이 됩니다. 이 공식에서 $\mathbf{\sqrt{n}}$으로 나눈다는 점을 주의하세요.
📂 라이트쎈 확통 답지 전체 모음 & 통계 공식 특강 (클릭)
표본평균의 분산($V(\bar{X})$)은 모분산($\sigma^2$)을 표본의 크기($n$)로 나눈 $\mathbf{\frac{\sigma^2}{n}}$ 이 됩니다. 이 공식에서 $\mathbf{\sqrt{n}}$으로 나눈다는 점을 주의하세요.
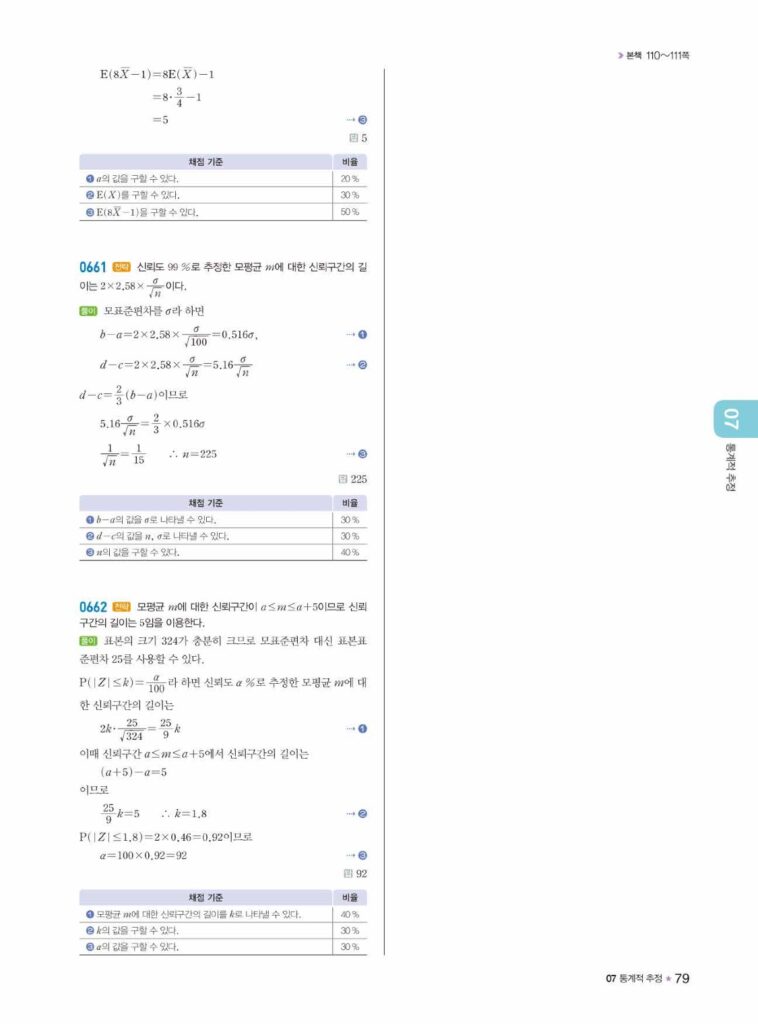
📖 통계적 추정 정답 및 해설
이미지를 클릭하면 확대됩니다.


🎁 신뢰구간의 길이, $k \frac{\sigma}{\sqrt{n}}$의 의미!
신뢰구간의 길이를 구하는 공식 $\mathbf{2 \cdot k \cdot \frac{\sigma}{\sqrt{n}}}$에서, $k$값(신뢰도)과 $\sqrt{n}$(표본 크기)의 관계를 이해해야 논리 문제에 대처할 수 있습니다.
👉 통계적 추정 공식 총정리 영상 보러가기