쎈 공통수학1 · 2단원 · 인수분해 활용 — 수의 계산
📘 0252번 — 인수분해 — 큰 수의 계산 (치환)
📋 이 포스팅에 포함된 것들
- 문제 분석 & 핵심 단서 찾기
- 단계별 친절한 풀이 설명
- 풀이 영상 (유튜브)
- 해설 이미지
- 외워두면 좋은 꿀팁 패턴
- 흔한 실수 경고
- 내신·수능 목표 풀이 시간
- 관련 개념 & 연산 워크시트 링크
🎬 풀이 영상
영상을 먼저 보고, 아래 풀이 설명과 함께 복습하면 효과가 2배예요! 😊
🔍 문제 분석 & 핵심 단서
[문제 요약]
(99999³+1)÷(99998×99999+1)의 값을 구하는 문제
(99999³+1)÷(99998×99999+1)의 값을 구하는 문제
🔑 이 문제의 핵심 단서는 바로 이것!
99999=a로 치환! 분자는 a³+1, 분모는 99998×99999+1=(a−1)a+1=a²−a+1. a³+1을 인수분해하면 분모와 약분됩니다!
✏️ 단계별 풀이 설명
1
99999=a로 치환
99999 = a로 놓으면:
분자: 99999³+1 = a³+1
분모: 99998×99999+1 = (a−1)·a+1 = a²−a+1
99999 = a로 놓으면:
분자: 99999³+1 = a³+1
분모: 99998×99999+1 = (a−1)·a+1 = a²−a+1
2
분자 인수분해
a³+1 = (a+1)(a²−a+1)
⚠️ a³+b³ = (a+b)(a²−ab+b²) → 가운데 부호 주의!
a³+1 = (a+1)(a²−a+1)
⚠️ a³+b³ = (a+b)(a²−ab+b²) → 가운데 부호 주의!
3
약분
(a+1)(a²−a+1) ÷ (a²−a+1)
= a+1
(a+1)(a²−a+1) ÷ (a²−a+1)
= a+1
4
최종 답
a+1 = 99999+1 = 100000 → 정답 ④
a+1 = 99999+1 = 100000 → 정답 ④
정답: 100000 (④)
💡 외워두면 좋은 꿀팁 패턴
🌟 이 유형의 황금 패턴
큰 수 계산 = 치환 신호! a=큰 수로 놓고 → 분자·분모를 a식으로 변환 → 인수분해 → 약분
⚠️ 이것만 조심하세요!
큰 수에 당황해서 치환을 떠올리지 못하거나, a³+1=(a+1)(a²−a+1) 공식에서 중간 항 부호를 잘못 쓰는 실수
⏱️ 목표 풀이 시간
시험장에서 이 문제를 만났을 때 아래 시간 안에 풀 수 있도록 연습하세요!
🏫 내신 시험
2~3분
계산 검토 시간 포함
📝 수능 시험
1~2분
패턴 암기로 시간 단축!
⚡ 시간 줄이는 법: 수치 계산 문제는 직접 대입 금지! 반드시 치환 또는 인수분해 먼저. 치환 후 약분되거나 인수분해 후 계산이 단순해지는 것을 확인하면 자신감이 생깁니다.
🖼️ 해설 이미지
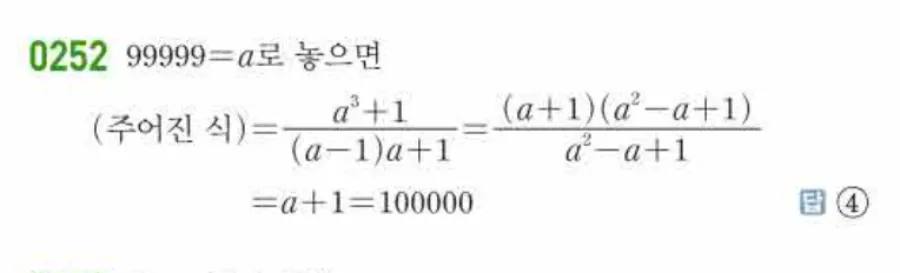
📚 관련 개념 포스트
✍️ 연산 워크시트 (기초 연습)
🎯 마플시너지 추천 문제
같은 개념을 다른 각도로 연습하고 싶다면 아래 마플시너지 포스트를 추천해요!
🗺️ 추천 학습 순서
✍️ 연산 워크시트
→
📖 개념 포스트
→
🎯 마플시너지
연산으로 기초 계산에 익숙해진 후 → 개념 포스트로 원리를 이해하고 → 마플시너지로 심화 문제에 도전하세요! 🚀