쎈 공통수학1 0057번 풀이 | (a+b)(b+c)(c+a) 값 구하기 | 쎈수학 답지

쎈 공통수학1 0057번 풀이

a+b+c=2, ab+bc+ca=−7, abc=−2일 때, (a+b)(b+c)(c+a)의 값

유형 03 · 곱셈공식을 이용한 전개 난이도 ⭐⭐상

📋 이 포스팅에 포함된 내용

풀이 영상 (동영상 해설)
해설 이미지 (쎈 공통수학1 답지)
문제 분석 및 단서 찾기
단계별 상세 풀이
꿀팁: 외워두면 좋은 패턴
흔한 실수 & 주의사항
시간 관리 전략
관련 개념 및 추천 링크

🎬 풀이 영상

대칭식의 핵심 변환 테크닉! 영상으로 먼저 흐름을 잡으세요.

🔍 문제 분석 — 단서 찾기

[문제 요약]
a+b+c = 2, ab+bc+ca = −7, abc = −2일 때,
(a+b)(b+c)(c+a)의 값은?

🔑 핵심 단서 포인트

1 조건이 3개, 미지수도 3개! — a+b+c, ab+bc+ca, abc 이 세 가지는 대칭식의 기본 3대장이에요!

2 (a+b), (b+c), (c+a)를 변환! — a+b+c = 2이므로 각 괄호를 (a+b+c)−c = 2−c 형태로 바꿀 수 있어요!

3 직접 전개 후 조건 대입! — (2−c)(2−a)(2−b)를 전개하면 조건으로 주어진 값들이 딱 맞게 들어가요!

📝 단계별 상세 풀이

Step 1. 각 괄호를 a+b+c를 이용해 변환

a+b+c = 2이므로:

a+b = 2-c b+c = 2-a c+a = 2-b

따라서:

(a+b)(b+c)(c+a) = (2-c)(2-a)(2-b)

Step 2. (2−a)(2−b)(2−c) 전개하기

세 괄호를 전개하면:

(2-a)(2-b)(2-c) = 8 - 4(a+b+c) + 2(ab+bc+ca) - abc

이 전개 공식은 어떻게 나온 걸까?

먼저 앞의 두 괄호를 곱하면:

(2−a)(2−b) = 4 − 2a − 2b + ab = 4 − 2(a+b) + ab

여기에 (2−c)를 곱하면:

{4−2(a+b)+ab}(2−c)

= 8 − 4c − 4(a+b) + 2c(a+b) + 2ab − abc

= 8 − 4(a+b+c) + 2(ab+bc+ca) − abc

Step 3. 조건 대입

= 8 - 4 \cdot 2 + 2 \cdot (-7) - (-2) = 8 - 8 - 14 + 2 = -12

✨ 정답: ① −12

📸 해설 이미지 (쎈 공통수학1 답지)

아래 이미지에서 0057번 풀이를 직접 확인해 보세요.

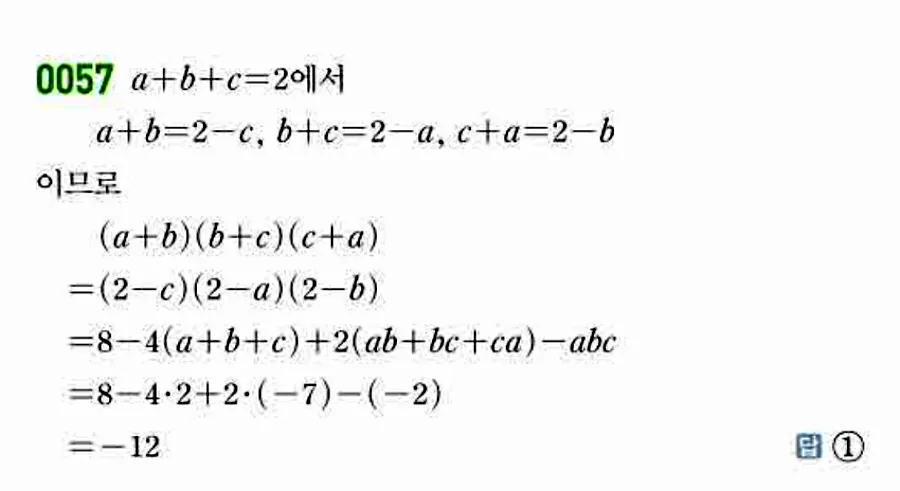
🍯 꿀팁 & 외워두면 좋은 패턴

🔥 필수 암기! (t−a)(t−b)(t−c) 전개 공식

(t−a)(t−b)(t−c)

= t³ − (a+b+c)t² + (ab+bc+ca)t − abc

이 공식은 대칭식 문제에서 거의 매번 쓰여요!

이 문제에서는 t = 2를 대입한 거예요:

= 8 − 4(a+b+c) + 2(ab+bc+ca) − abc

대칭식의 기본 3대장 — 반드시 정리!

세 변수 a, b, c에 대한 조건이 다음 형태로 주어지면 대칭식 문제예요:

① a+b+c (합)

② ab+bc+ca (두 개씩 곱의 합)

③ abc (세 개의 곱)

🔥 이 3개만 알면 a, b, c에 대한 모든 대칭식의 값을 구할 수 있어요!

“a+b = (a+b+c) − c” 변환 — 자주 쓰이는 테크닉

a+b+c의 값이 주어져 있을 때, a+b, b+c, c+a는 각각:

· a+b = (a+b+c) − c

· b+c = (a+b+c) − a

· c+a = (a+b+c) − b

이 변환을 통해 (a+b)(b+c)(c+a)를 조건으로 바로 계산할 수 있는 형태로 바꿔요!

⚠️ 흔한 실수 & 주의사항

실수 1: abc = −2에서 부호 실수

마지막 항이 −abc이므로, −(−2) = +2예요. 이중 부호를 놓치면 답이 −16이 되어 틀려요!

실수 2: 전개 공식의 부호 패턴 혼동

(t−a)(t−b)(t−c)의 전개에서 부호는 +, −, +, − 교대예요:

t³ − (합)t² + (쌍곱의합)t − abc

부호를 하나라도 잘못 쓰면 답이 크게 달라져요!

실수 3: a, b, c 각각의 값을 구하려고 하는 경우

이 문제에서 a, b, c 각각의 값을 구할 필요가 전혀 없어요! 대칭식 3대장의 값만으로 충분히 풀 수 있어요. 개별 값을 구하려다 시간만 낭비하게 돼요.

⏱️ 시간 관리 전략

목표 풀이 시간

내신 시험: 3~4분

수능/모의고사: 2~3분

시간을 줄이려면?

1 (t−a)(t−b)(t−c) 전개 공식 암기: 이 공식을 외워두면 전개 과정 없이 바로 조건을 대입할 수 있어요.

2 “a+b = (합) − c” 변환 반사적으로: 문제를 보자마자 이 변환을 떠올리는 훈련을 하세요.

3 부호 계산은 천천히, 정확하게: 이 유형에서 속도보다 중요한 것은 부호 정확성이에요. 1분을 더 쓰더라도 부호를 확실히 하세요.

📚 더 공부하기 — 추천 순서

📝 연산 워크시트 (기초 다지기)

공통수학1 연산 05. 곱셈 공식 (1) 공통수학1 연산 06. 곱셈 공식 (2) 공통수학1 연산 07. 곱셈 공식의 변형 공통수학1 연산 08. 곱셈 공식의 활용

🚀 마플시너지 공통수학1 (심화 도전)

마플시너지 0073번 | 다항식 곱셈 완벽정리 마플시너지 0058번 | 항등식 특수값 대입 빠른풀이 마플시너지 097번 | 항등식 계수비교 마플시너지 098번 | 부정계수법 다항식나눗셈

💪 대칭식 3대장(합, 쌍곱합, 곱)만 알면 모든 대칭식 문제가 풀려요!
“(t−a)(t−b)(t−c) 전개 공식” 하나 외우면 이 유형은 완벽! 화이팅! 🎯

쎈공통수학1답지57번일반항의 합 | a + b + c = 2, ab + bc + ca = -7일 때 (a+b)(b+c)(c+a) 구하기