쎈 공통수학1 40번 풀이 해설
💡 잠깐! 2X − B = A − 5B 를 X에 대해 먼저 정리해 보셨나요?
스스로 풀어본 후 정답을 확인하면 학습 효과가 2배입니다.
👇 아래에서 영상 풀이 → 실수 포인트 → 정답 & 해설 순서로 확인하세요
스스로 풀어본 후 정답을 확인하면 학습 효과가 2배입니다.
👇 아래에서 영상 풀이 → 실수 포인트 → 정답 & 해설 순서로 확인하세요
영상 풀이
📺 영상으로 보면 풀이 과정을 단계별로 더 쉽게 이해할 수 있습니다
왜 이렇게 풀어야 할까?
🧠 풀이 전략의 이유
이 문제에서 A, B에 직접 다항식을 대입한 뒤 정리하면 계산이 복잡해지고 실수가 생기기 쉽습니다. 반드시 X = (식) 꼴로 먼저 정리한 뒤 대입하는 것이 정석입니다.
올바른 풀이 순서:
❶ 2X − B = A − 5B 에서 X에 대해 정리
→ 2X = A − 5B + B = A − 4B
→ X = ½A − 2B
❷ A, B 대입
→ ½(2x²−4xy+6y²) − 2(−x²+2xy+4y²)
❸ 분배법칙 적용 후 동류항 정리
→ (x²−2xy+3y²) + (2x²−4xy−8y²)
→ 3x² − 6xy − 5y²
❶ 2X − B = A − 5B 에서 X에 대해 정리
→ 2X = A − 5B + B = A − 4B
→ X = ½A − 2B
❷ A, B 대입
→ ½(2x²−4xy+6y²) − 2(−x²+2xy+4y²)
❸ 분배법칙 적용 후 동류항 정리
→ (x²−2xy+3y²) + (2x²−4xy−8y²)
→ 3x² − 6xy − 5y²
이 순서를 지키면 계산량이 줄고, 실수 위험도 크게 낮아집니다. 다항식 문제에서 “미지수를 먼저 분리한다”는 원칙은 이후 연립방정식, 행렬 등에서도 계속 쓰이는 중요한 습관입니다.
실수 포인트 & 방지법
🚨 학생들이 자주 틀리는 포인트
실수 ① 이항 부호 오류
2X − B = A − 5B 에서 B를 이항할 때 −5B + B = −4B인데, 부호를 놓쳐서 −6B 또는 −5B로 계산하는 경우가 많습니다.
실수 ② 분배법칙에서 부호 실수
−2 × B 에서 B = −x²+2xy+4y² 이므로 −2 × (−x²) = +2x² 입니다. 음수 × 음수 = 양수를 놓치면 답이 완전히 달라집니다.
실수 ③ ½ 분배 누락
X = ½A − 2B 에서 ½을 A의 모든 항에 곱해야 합니다. 앞의 x² 항에만 ½을 곱하고 뒤의 항은 그대로 쓰는 실수가 빈번합니다.
✅ 실수를 줄이는 3가지 습관
습관 1 — 정리 먼저, 대입 나중에:
다항식이 포함된 등식은 반드시 X = (식) 형태로 완전히 정리한 후에 대입하세요.
습관 2 — 괄호를 끝까지 유지:
−2(−x²+2xy+4y²)에서 괄호를 풀 때 각 항마다 부호를 하나씩 확인하며 쓰세요.
한꺼번에 암산하면 부호 실수 확률이 3배 높아집니다.
습관 3 — 동류항 밑줄 표시:
x²항, xy항, y²항을 각각 다른 표시(밑줄, 동그라미, 네모)로 구분하면
정리할 때 빠뜨리는 항이 없어집니다.
정답 확인
40번 정답
③
X = 3x² − 6xy − 5y²
풀이 해설
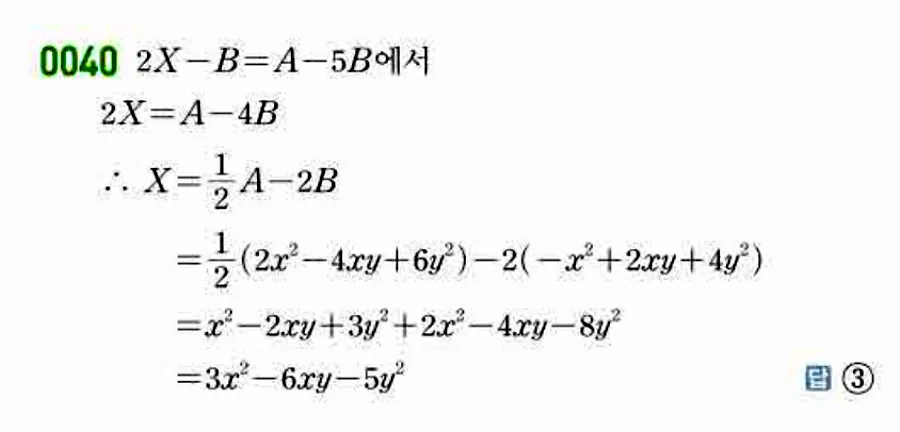
🎯 한줄 풀이 포인트
등식을 X에 대해 먼저 정리한 뒤, A와 B를 대입하여 동류항끼리 계산하는 문제입니다. 다항식을 숫자처럼 이항·정리하는 감각이 핵심입니다.
함께 풀면 좋은 문제
40번과 같은 다항식의 덧셈과 뺄셈 유형을 집중 연습할 수 있는 연산 워크시트입니다. 프린트해서 직접 풀어보세요.
💡 추천 순서: 기본(정리) → 핵심(덧셈뺄셈) → 심화(곱셈) 순으로 풀면 실수율이 확 줄어듭니다