“

[문제 828] 핵심 개념 및 풀이 전략

주어진 집합 연산과 동치인 표현을 찾는 문제입니다.

접근법:
1. 주어진 식 (Aᶜ∪B) – A 를 간단히 합니다.
– (Aᶜ∪B) ∩ Aᶜ
– (Aᶜ∩Aᶜ) ∪ (B∩Aᶜ) = Aᶜ ∪ (B-A)
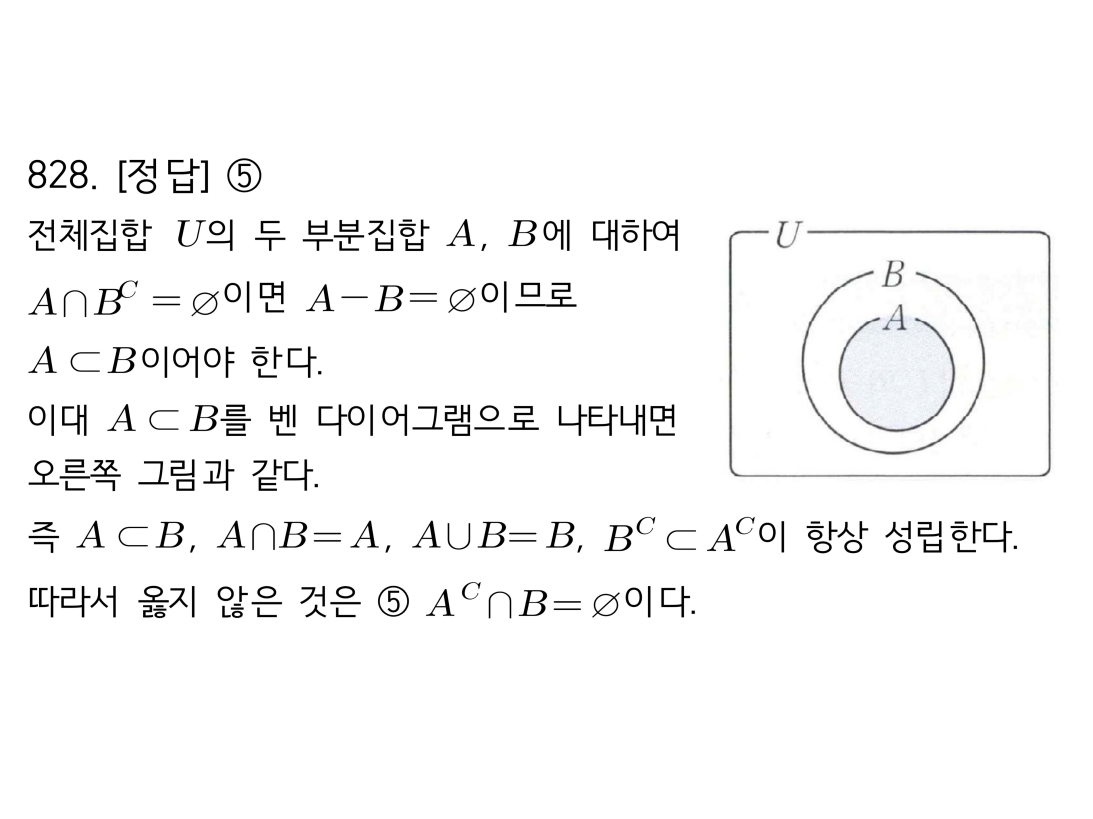
2. 벤 다이어그램을 그려보면, A의 바깥 부분과 B에만 속하는 부분을 합친 영역입니다.
3. 각 보기의 식을 간단히 하거나 벤 다이어그램으로 그려서 2번의 영역과 일치하는 것을 찾습니다.
– ⑤ (A∩B)ᶜ = Aᶜ∪Bᶜ. 벤 다이어그램을 그려보면 두 영역이 다릅니다. (해설에서는 ⑤가 답이므로 문제나 해설에 오류가 있을 수 있음)

주의할 점:
복잡한 집합 연산의 동치 관계를 찾을 때는, 벤 다이어그램을 이용하는 것이 실수를 줄이는 가장 확실한 방법입니다.

”

세 집합의 복잡한 연산과 벤 다이어그램