“

[문제 759] 핵심 개념 및 풀이 전략

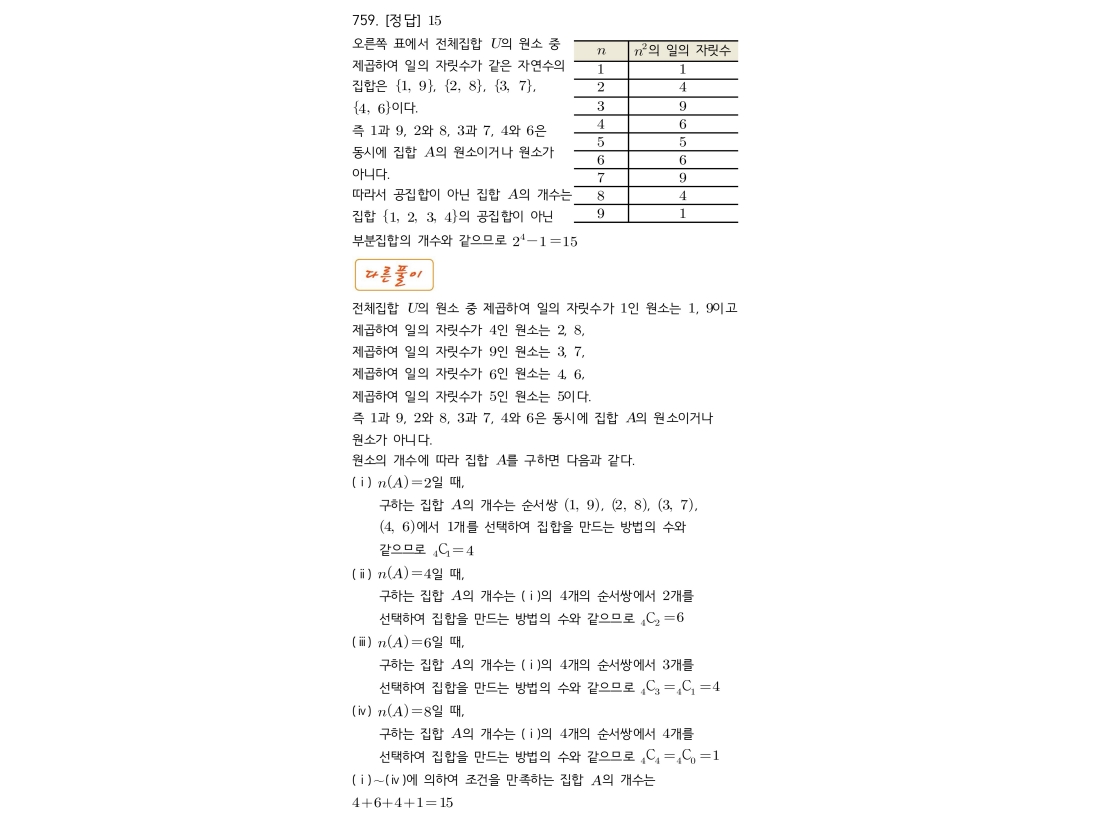
제곱수의 일의 자리 수에 대한 규칙을 만족하는 집합의 개수를 찾는 문제입니다.

접근법:
1. 1부터 9까지의 자연수에 대해, m과 m²의 일의 자릿수가 같은 m이 아닌 n이 존재하는지 확인하여 원소 쌍을 찾습니다.
– m=2 (2²=4), n=8 (8²=64) → {2,8}은 쌍으로 존재
– m=3 (3²=9), n=7 (7²=49) → {3,7}은 쌍으로 존재
– {1,9}, {4,6}도 같은 규칙으로 쌍을 이룹니다.
– 5는 자기 자신과 짝이므로 규칙에 맞지 않습니다.
2. 이 규칙을 만족하는 집합 A는, 4개의 묶음({1,9}, {2,8}, {3,7}, {4,6})을 원소로 하는 새로운 집합의 부분집합과 같습니다.
3. 4개의 묶음으로 만들 수 있는 부분집합의 개수는 2⁴개 입니다.
4. 문제에서 공집합이 아닌 집합을 구하라고 했으므로 1개를 제외합니다.

주의할 점:
문제의 규칙을 만족하는 원소 쌍을 정확하게 찾는 것이 첫 단계입니다. 규칙에 맞지 않는 원소(5)는 집합 A에 포함될 수 없습니다.

”

제곱수의 일의 자리 수 규칙을 갖는 집합 찾기