“

[문제 682] 핵심 개념 및 풀이 전략

한 집합의 원소를 더하여 만들어지는 새로운 집합의 합을 이용해, 원래 집합의 원소를 찾는 문제입니다.

접근법:
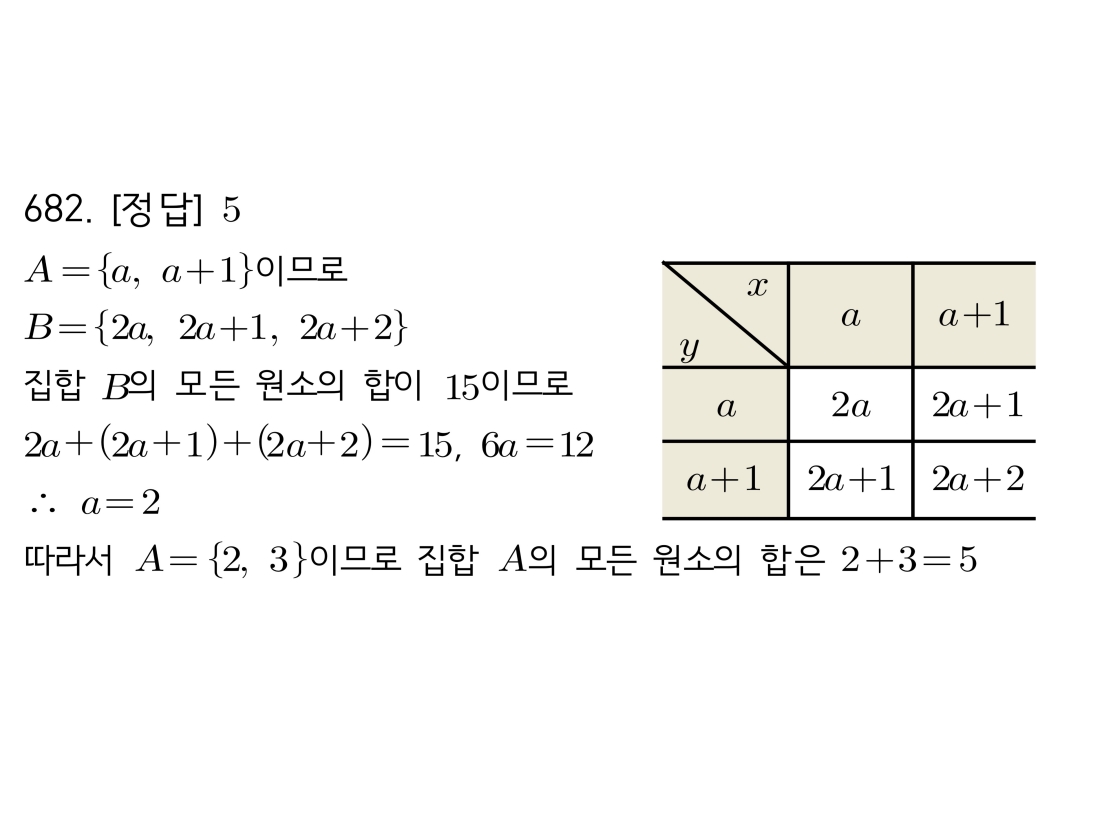
1. 집합 A={a, a+1}의 원소 x, y를 이용하여 집합 B의 원소를 구합니다.
– x=a, y=a → x+y = 2a
– x=a, y=a+1 → x+y = 2a+1
– x=a+1, y=a+1 → x+y = 2a+2
– B = {2a, 2a+1, 2a+2}
2. 집합 B의 모든 원소의 합이 15라고 했으므로, (2a)+(2a+1)+(2a+2) = 15 라는 방정식을 풉니다.
3. a값이 결정되면 집합 A의 원소를 확정하고, 그 원소들의 합을 구합니다.

주의할 점:
집합 B의 원소를 구할 때, x와 y가 같을 수도 있다는 점(x∈A, y∈A)을 고려해야 합니다.

”

두 집합 원소의 합으로 만들어진 새 집합