마플시너지공통수학2풀이해설0640고퀄리티 풀이영상제공0640 대칭이동과 원의 최대/최소 거리

“

[문제 640] 핵심 개념 및 풀이 전략

평행이동을 통해 최단 거리를 구하는 문제입니다. 강을 건너는 문제의 대표적인 유형입니다.

접근법:
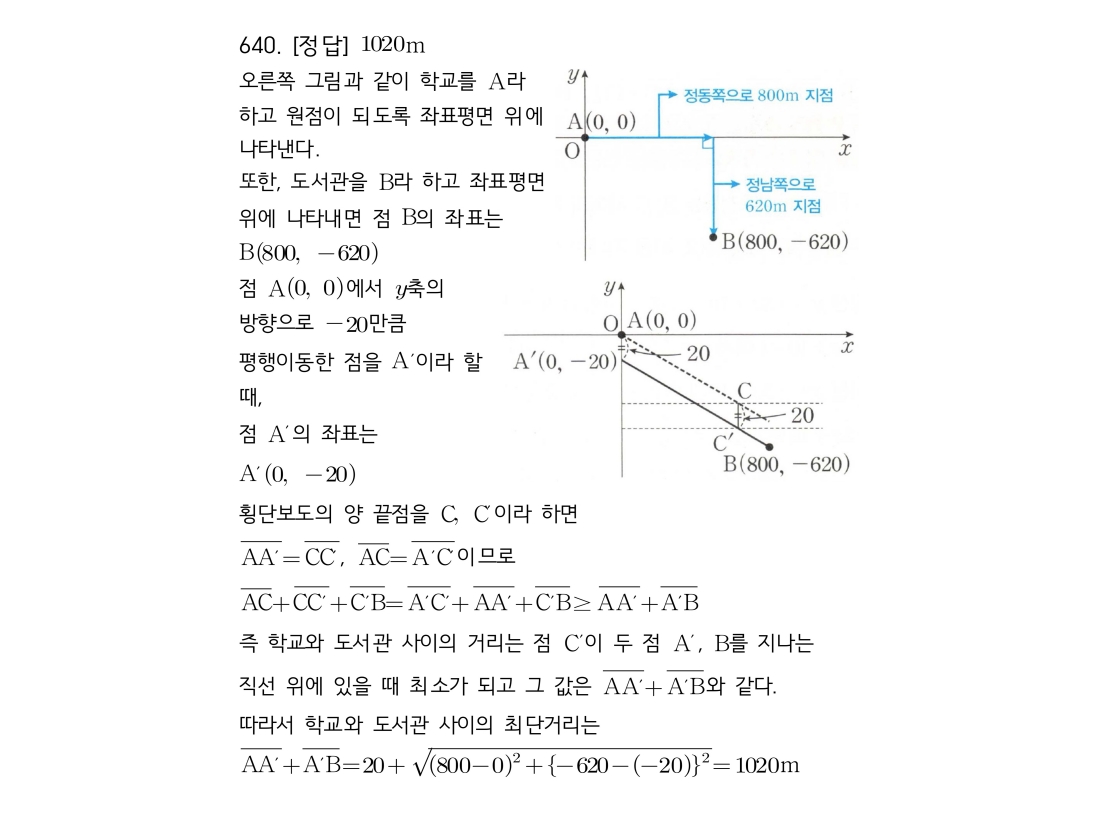
1. 횡단보도를 건너는 것은 y축 방향으로 20만큼 이동하는 것과 같습니다.
2. 학교 A와 도서관 B 사이의 최단 거리를 구하기 위해, 한 점(예: 학교 A)을 횡단보도의 이동 벡터만큼 **평행이동** 시킵니다.
3. 즉, 학교 A를 y축 방향으로 -20만큼 평행이동한 점 A’을 구합니다.
4. 최단 거리는 **평행이동한 점 A’과 원래 점 B 사이의 직선 거리**에 **횡단보도의 길이(20m)**를 더한 값입니다.

주의할 점:
강이나 도로처럼 폭이 있는 장애물을 건너는 최단 거리는, 대칭이동이 아닌 평행이동을 이용한다는 점을 기억해야 합니다.

”

대칭이동과 원의 최대/최소 거리