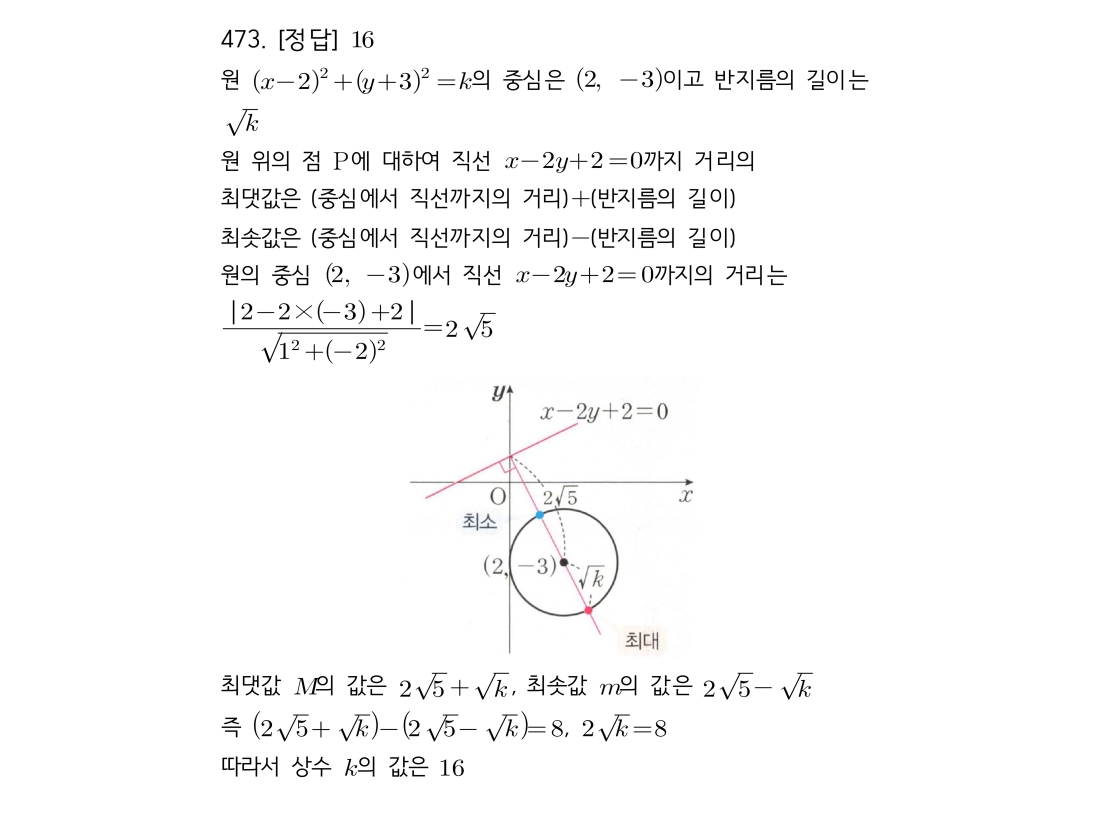
“

[문제 473] 핵심 개념 및 풀이 전략

원 위의 점과 직선 사이의 거리의 최댓값(M)과 최솟값(m)의 관계를 이용하는 문제입니다.

접근법:
1. 원 위의 점에서 직선까지의 거리의 최댓값은 **M = d + r**, 최솟값은 **m = d – r** 입니다. (d: 중심과 직선 사이 거리, r: 반지름)
2. 따라서 M – m = (d+r) – (d-r) = **2r** 이라는 중요한 관계식이 성립합니다.
3. 문제에서 M-m=8 이라고 주어졌으므로, 2r = 8, 즉 반지름 r=4 임을 알 수 있습니다.
4. 원의 방정식에서 반지름은 √k 이므로, k=16 이 됩니다.

주의할 점:
최댓값과 최솟값의 차이는 항상 ‘지름의 길이(2r)’와 같다는 사실을 알고 있으면 매우 빠르고 간단하게 풀 수 있는 문제입니다.

”

정점을 지나는 직선과 원 위 점 거리 최댓값