“

[문제 351] 핵심 개념 및 풀이 전략

정점과 원 위의 동점을 잇는 선분의 중점이 그리는 도형, 즉 자취의 방정식을 찾는 문제입니다.

접근법:
1. 구하려는 중점의 좌표를 (x,y), 원 위의 점 P의 좌표를 (a,b)로 설정합니다.
2. 중점 공식을 이용해 a와 b를 각각 x와 y에 대한 식으로 표현합니다. (예: a=2x+4)
3. 점 P(a,b)는 원래 원 위의 점이므로, 원의 방정식에 a,b를 대입하면 성립합니다.
4. 이 원의 방정식에 2단계에서 구한 식을 대입하여 a,b를 소거하면, x와 y에 대한 새로운 원의 방정식이 만들어집니다.
5. 문제에서 요구하는 ‘도형의 길이’는 이 새로운 원의 둘레의 길이입니다.

주의할 점:
이러한 중점의 자취는 항상 원래 원과 닮음인 원이 되며, 반지름의 길이는 원래 원의 절반이 됩니다. 이 성질을 알고 있으면 검산에 유용합니다.

”

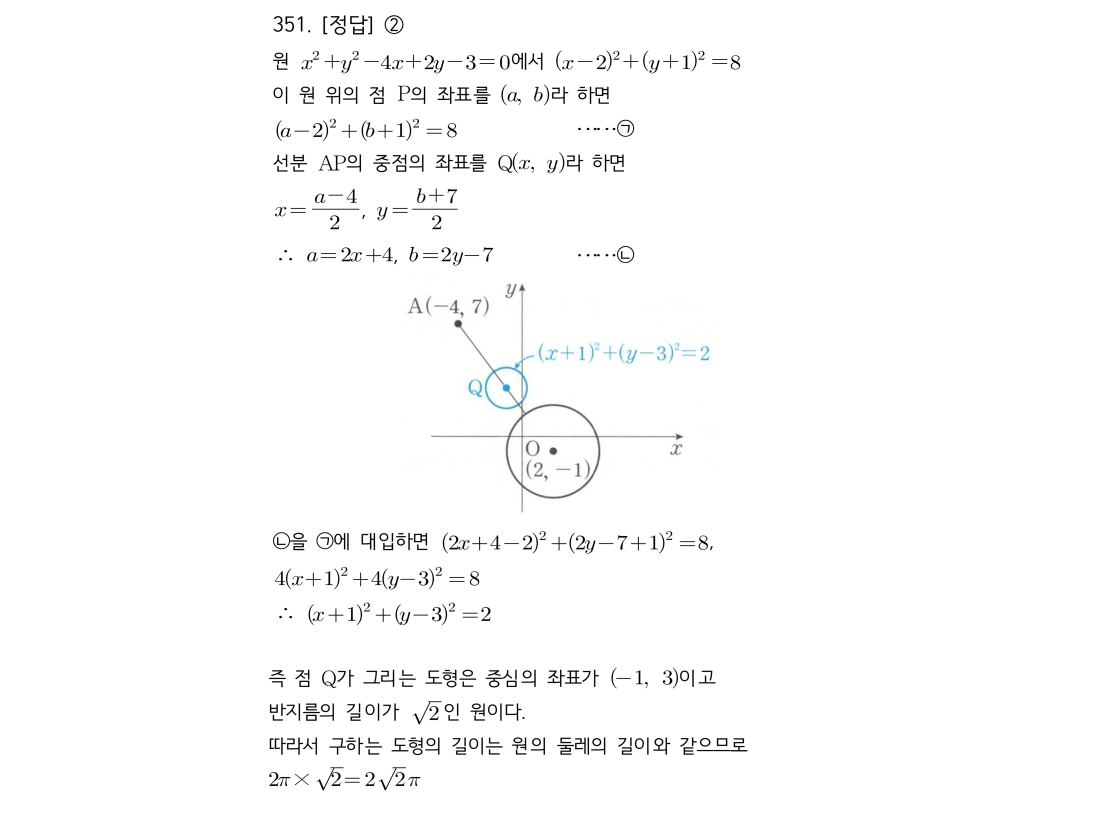
선분 중점의 자취의 방정식