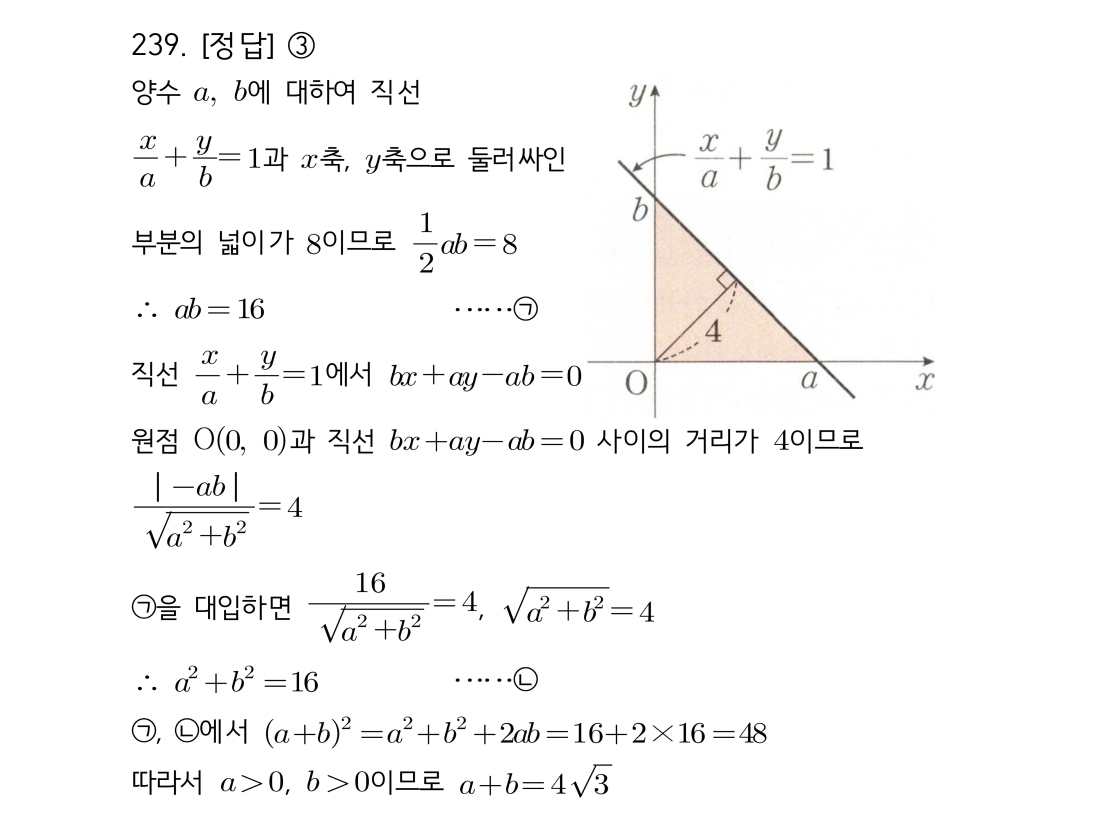
“

[문제 239] 핵심 개념 및 풀이 전략

직선과 좌표축으로 둘러싸인 삼각형의 넓이와, 원점과 직선 사이의 거리라는 두 가지 조건이 주어진 문제입니다.

접근법:
1. x절편 a, y절편 b인 직선이므로, 삼각형의 넓이는 1/2 * ab = 8 이라는 관계식을 얻습니다.
2. 원점 (0,0)과 직선 (bx+ay-ab=0) 사이의 거리가 4라는 조건을 점과 직선 사이의 거리 공식을 이용해 식으로 세웁니다.
3. 1, 2단계에서 얻은 두 개의 식(ab=16, a²+b²=16)을 연립하여 a+b의 값을 구합니다. 곱셈 공식의 변형을 활용하면 편리합니다.

주의할 점:
넓이와 원점에서의 거리라는 두 기하학적 조건을 각각 대수적인 식으로 정확히 변환하고, 이를 연립하여 푸는 능력이 필요합니다.

”

한 점에서 두 직선까지 거리가 같을 조건