“

[문제 154] 핵심 개념 및 풀이 전략

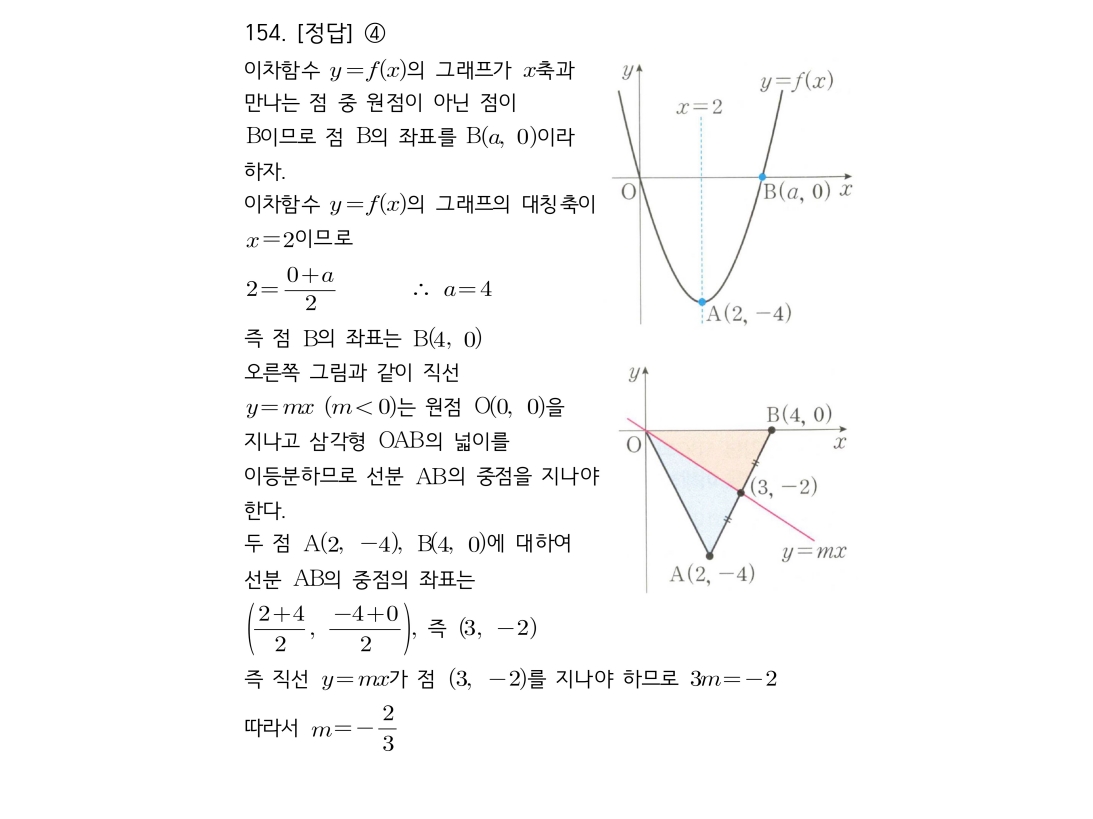
이차함수의 그래프와 x축으로 둘러싸인 삼각형의 넓이를 원점을 지나는 직선이 이등분하는 문제입니다.

접근법:
1. 먼저 이차함수의 꼭짓점 A와 x축과의 교점(원점 O, 점 B)의 좌표를 구합니다. 꼭짓점의 x좌표는 대칭축이므로, 이를 이용해 점 B의 좌표를 쉽게 찾을 수 있습니다.
2. 삼각형 OAB의 넓이를 이등분하는 직선 y=mx는 꼭짓점 O를 지납니다.
3. 따라서 이 직선은 반드시 대변 AB의 중점 M을 지나야 합니다.
4. 중점 M의 좌표를 구한 뒤, 이 좌표를 y=mx에 대입하여 기울기 m을 구합니다.

주의할 점:
이차함수의 대칭성을 이용하여 x절편을 찾는 것이 계산을 간편하게 합니다. 150번 문제와 마찬가지로, 넓이 이등분선은 대변의 중점을 지난다는 성질을 이용하는 것이 핵심입니다.

”

이차함수와 축으로 생긴 넓이 이등분