“

[문제 26] 핵심 개념 및 풀이 전략

25번 문제와 완전히 동일한 원리를 적용하는 문제입니다. 점의 좌표만 바뀌었습니다.

접근법:
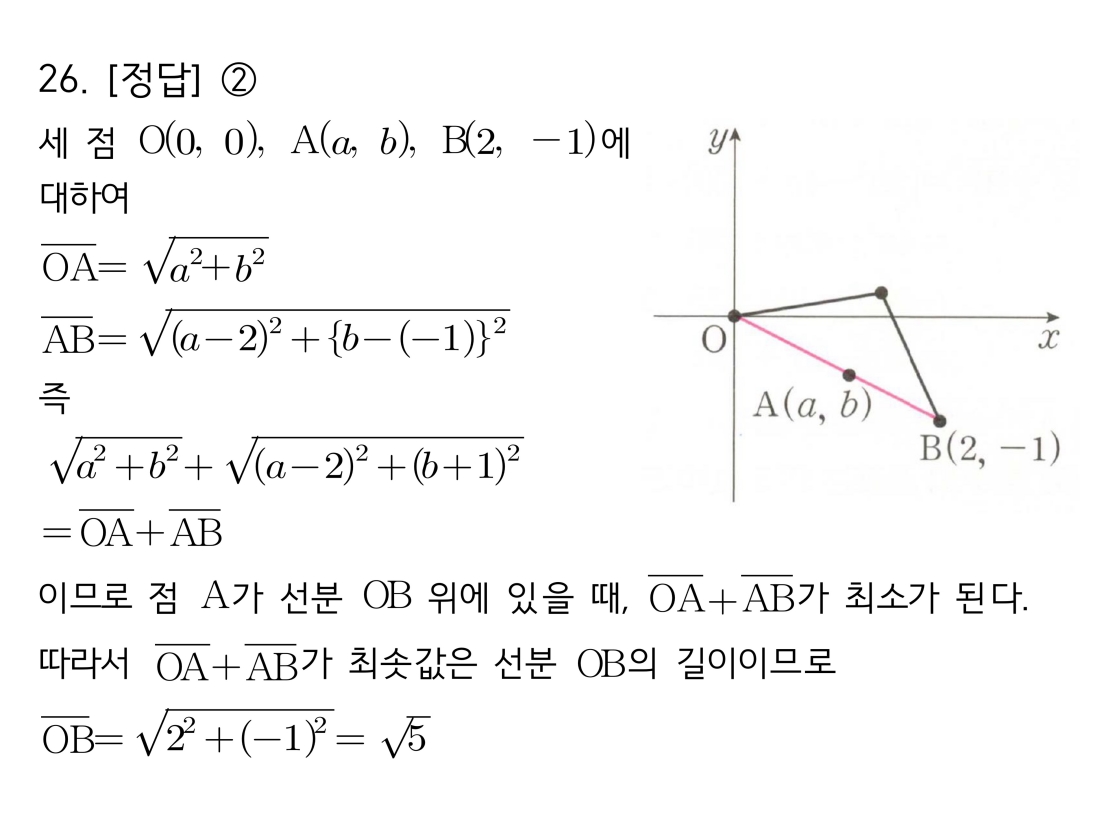
1. [cite_start]문제의 식은 원점 O(0,0)과 점 A(a,b) 사이의 거리, 그리고 점 A(a,b)와 점 B(2,-1) 사이의 거리의 합을 의미합니다. [cite: 1170-1174]
2. 이 거리의 합(OA+AB)이 최소가 되려면, 세 점 O, A, B가 **일직선 위에 있어야** 하며, 점 A는 선분 OB 위에 있어야 합니다.
3. 따라서 최솟값은 **선분 OB의 길이**와 같습니다. 원점 O와 점 B 사이의 거리를 구하면 됩니다.

주의할 점:
미지수 a, b가 포함되어 있어 복잡해 보이지만, 기하학적 의미를 파악하면 실제 계산은 매우 간단해지는 문제입니다. 식의 구조를 파악하는 것이 중요합니다.

”

세 점 사이 거리 합 최솟값