“

[문제 24] 핵심 개념 및 풀이 전략

루트가 포함된 복잡한 식의 최솟값을 좌표평면 위의 두 점 사이의 거리의 합으로 해석하여 푸는 문제입니다.

접근법:
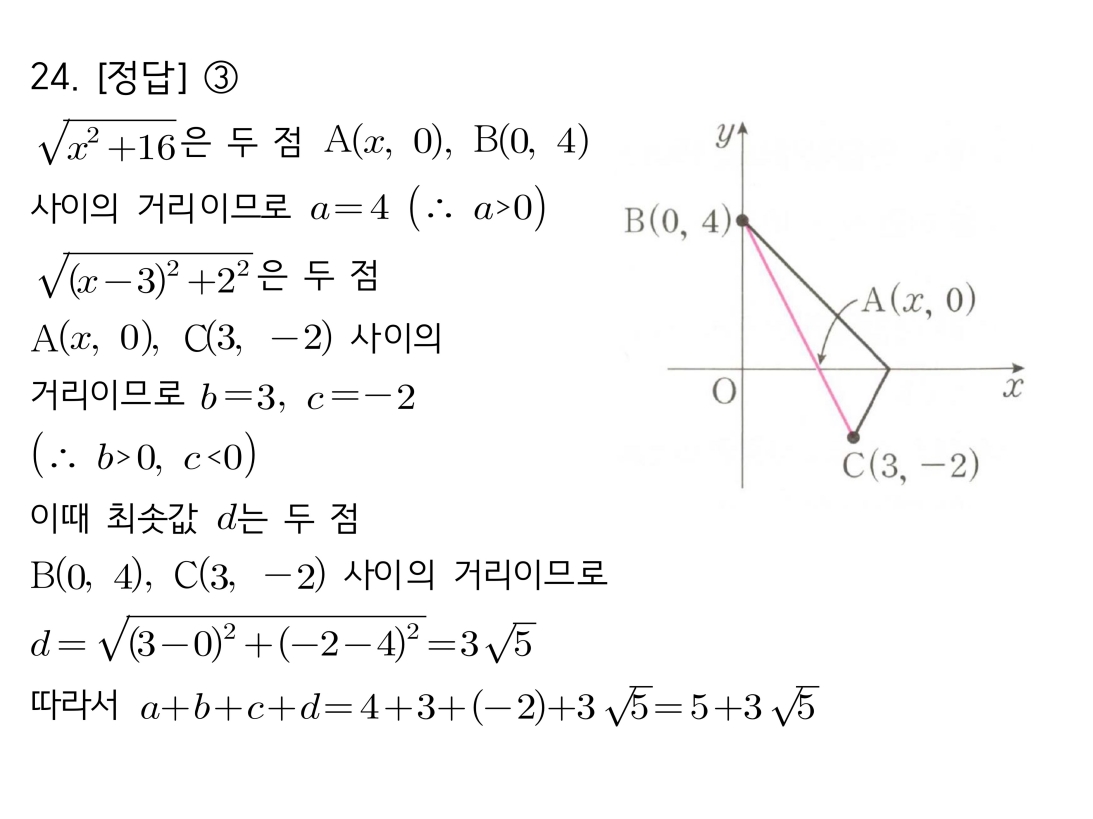
1. 식의 각 항을 두 점 사이의 거리로 해석합니다. [cite_start]첫 번째 항은 (x,0)과 (0,4) 사이의 거리, 두 번째 항은 (x,0)과 (3,-2) 사이의 거리로 볼 수 있습니다. [cite: 1137-1146]
2. 즉, 이 문제는 x축 위의 한 점(x,0)에서 두 정점(0,4), (3,-2)에 이르는 거리의 합의 최솟값을 구하는 것과 같습니다.
3. 거리의 합이 최소가 되는 경우는 **세 점이 일직선 위에 있을 때**이므로, 최솟값은 두 정점 (0,4)와 (3,-2) 사이의 거리와 같습니다.

주의할 점:
주어진 식을 그대로 계산하는 것이 아니라, 좌표평면 위의 선분의 길이로 기하학적인 의미를 부여하여 해석하는 능력이 필요합니다.

”

거리의 합 최솟값 (좌표 설정)