1440
2022년 06월 고1 학력평가 28번
정답 10
🔑 핵심 단서
인수분해 첫째 식 → (x − a²)(x + 3) < 0, 둘째 식 → (x + a)(x − 9) > 0
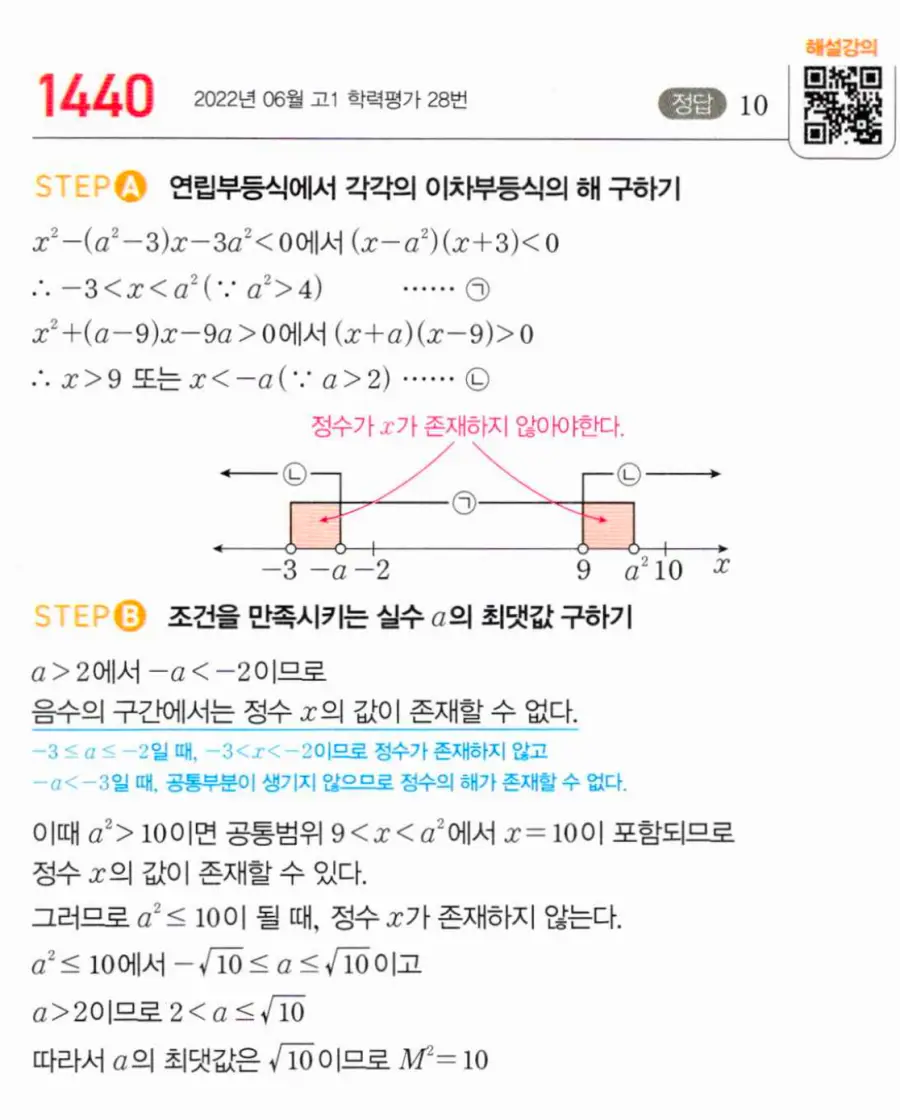
해 구간 a > 2이므로 수직선 위 두 해의 공통 구간에 정수가 없어야 합니다.
경계 음수 쪽은 정수 없음 확인 완료. 양수 쪽 9 < x < a²에서 a² ≤ 10이면 정수 10 미포함.
💡 왜 이렇게 풀어야 하는가
본질은 “공통 해 구간 안에 정수 없음”을 a 조건으로 번역하는 것입니다.
a > 2이므로 음수 구간 −3 < x < −a에서 −a < −2 → 정수 없음.
양수 구간 9 < x < a²에 정수 10이 안 들어가려면 a² ≤ 10. 열린 부등호이므로 a² = 10일 때 x = 10 미포함 → 등호 성립.
∴ M = √10, M² = 10
① 인수분해
② 해 구간
③ 수직선 공통구간
④ 정수 조건 → a 범위
📺 해설 강의
📝 해설 이미지
클릭하면 원본 크기로 열립니다
⚠️ 자주 하는 실수
음수 구간을 안 보고 양수만 검토 — 변형 문제에선 음수 쪽이 핵심일 수 있음
a² ≤ 9로 잘못 세움 — 9 < x < a²이므로 정수 10 미포함 조건은 a² ≤ 10
열림/닫힘 혼동 — < 0이므로 경계 x = a²는 해에 미포함, 등호 가능
a > 2 조건을 잊고 a = 1 대입 → 해 방향 뒤집힘
2 < a ≤ √10 → M = √10 → M² = 10