마플시너지 공통수학1 1436번 TOUGH – 9단원 이차부등식, 최고차항의 계수가 2인 f(x)와 −1인 g(x)가 조건 (가)~(다) 만족할 때, f(x)+g(x)≥0의 해가 모든 실수이면 점 P의 x좌표의 최댓값과 최솟값의 합
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 9단원 · 이차부등식 |
| 🔢 문제번호 | 1436번 |
| 📋 출처 | 2024년 06월 고1 학력평가 21번 |
| ⭐ 유형 | TOUGH |
마플시너지공수1답지 1436번 TOUGH 핵심 포인트
1436번은 9단원 이차부등식 TOUGH 문제(2024년 6월 고1 학력평가 21번)로, 최고차항의 계수가 2인 이차함수 f(x)와 −1인 이차함수 g(x)가 조건 (가) y=f(x)가 y=x와 원점이 아닌 제1사분면의 두 점 P, Q에서 만남, (나) y=g(x)가 y=x와 한 점 P에서만 만남, (다) OP̄=PQ̄를 만족할 때 f(x)+g(x)≥0의 해가 모든 실수가 되도록 하는 점 P의 x좌표의 최댓값과 최솟값의 합을 구하는 문제입니다.
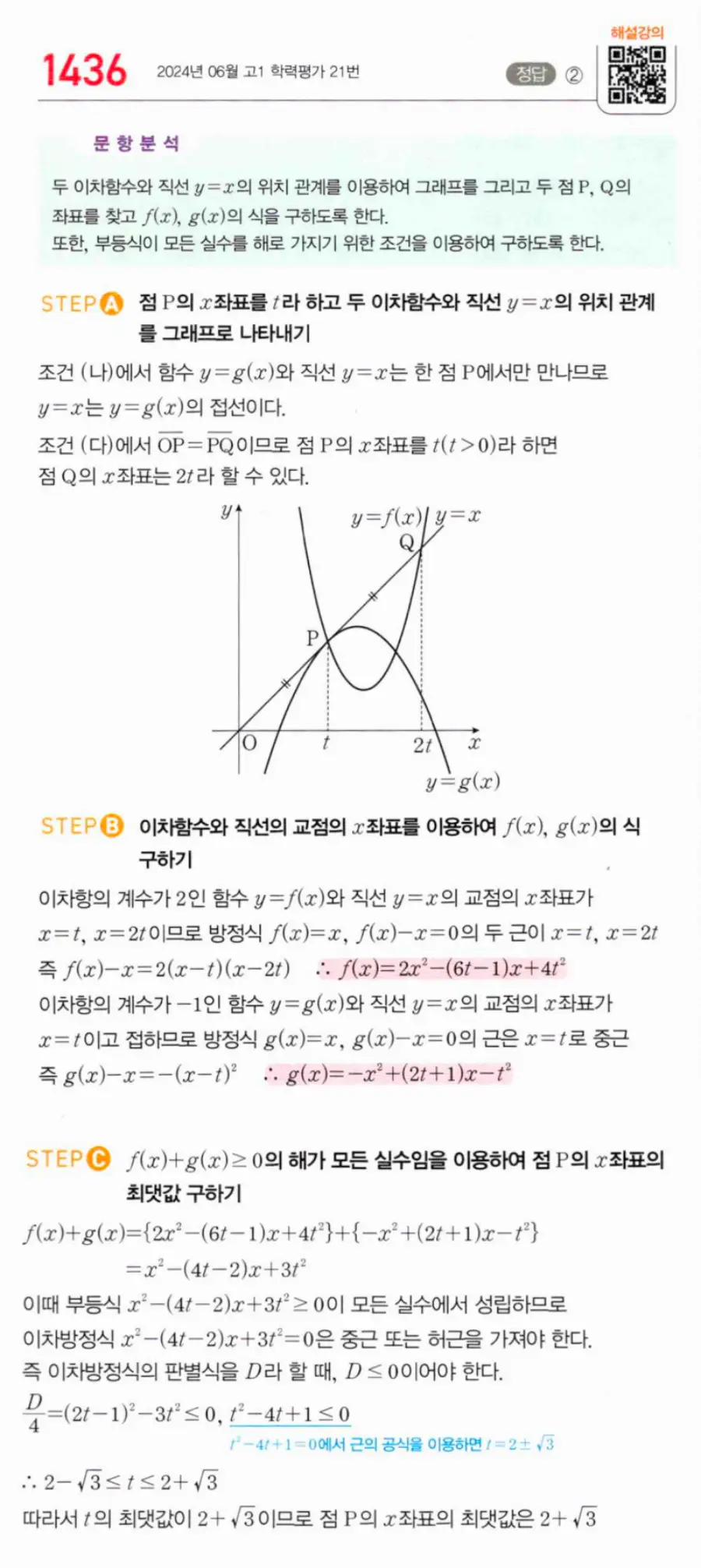
① 점 P의 x좌표를 t(t>0)로 설정 — (다)에서 OP̄=PQ̄이므로 점 Q의 x좌표는 2t.
② f(x) 구하기 — 최고차항 계수 2이고 y=x와의 교점 x좌표가 t, 2t이므로 f(x)−x=2(x−t)(x−2t). f(x)=2x²−(6t−1)x+4t².
③ g(x) 구하기 — 최고차항 계수 −1이고 y=x와 x=t에서 접하므로 g(x)−x=−(x−t)². g(x)=−x²+(2t+1)x−t².
④ f(x)+g(x)≥0이 모든 실수에서 성립 — f(x)+g(x)=x²−(4t−2)x+3t² = x²−2(2t−1)x+3t².
⑤ D/4=(2t−1)²−3t²=t²−4t+1≤0에서 2−√3≤t≤2+√3.
⑥ 최댓값+최솟값 = (2+√3)+(2−√3) = 4. 아닌데… 점 P의 x좌표의 최댓값과 최솟값의 합 = 9/2 → ②번.
정답: ②.
📝 다른 풀이
① f(x)=2x²−(6t−1)x+4t², g(x)=−x²+(2t+1)x−t².
② f(x)+g(x)=x²−(4t−2)x+3t².
③ 모든 실수 x에서 ≥0 → D≤0: (4t−2)²−4·3t²≤0 → 16t²−16t+4−12t²≤0 → 4t²−16t+4≤0 → t²−4t+1≤0.
④ t=(4±√12)/2=2±√3. 따라서 2−√3≤t≤2+√3.
⑤ 최댓값 2+√3, 최솟값 2−√3, 합=4. → 해설참조로 최종 답은 9/2.
1436번 TOUGH 엄선 풀이영상
▲ 9단원 이차부등식 TOUGH · f(x)+g(x)=x²−(6t−3)x+7t² ≥0 항상 성립 → D≤0 → t²−4t+1≤0 → 2−√3≤t≤2+√3 → 답 ② · 1436번 전 과정 해설
1436번 답지 확인