🔥 TOUGH
📋 최다빈출 왕중요
마플시너지 공통수학1 1368번 TOUGH – 9단원 이차부등식, 세 실수 x−1, x, x+1이 예각삼각형의 세 변의 길이가 되도록 하는 x의 값의 범위
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 9단원 · 이차부등식 |
| 🔢 문제번호 | 1368번 |
| ⭐ 유형 | TOUGH |
마플시너지공수1답지 1368번 TOUGH 핵심 포인트
1368번은 9단원 이차부등식 TOUGH · 최다빈출 왕중요 문제로, 세 실수 x−1, x, x+1이 예각삼각형의 세 변의 길이가 되도록 하는 x의 값의 범위를 구하는 문제입니다.
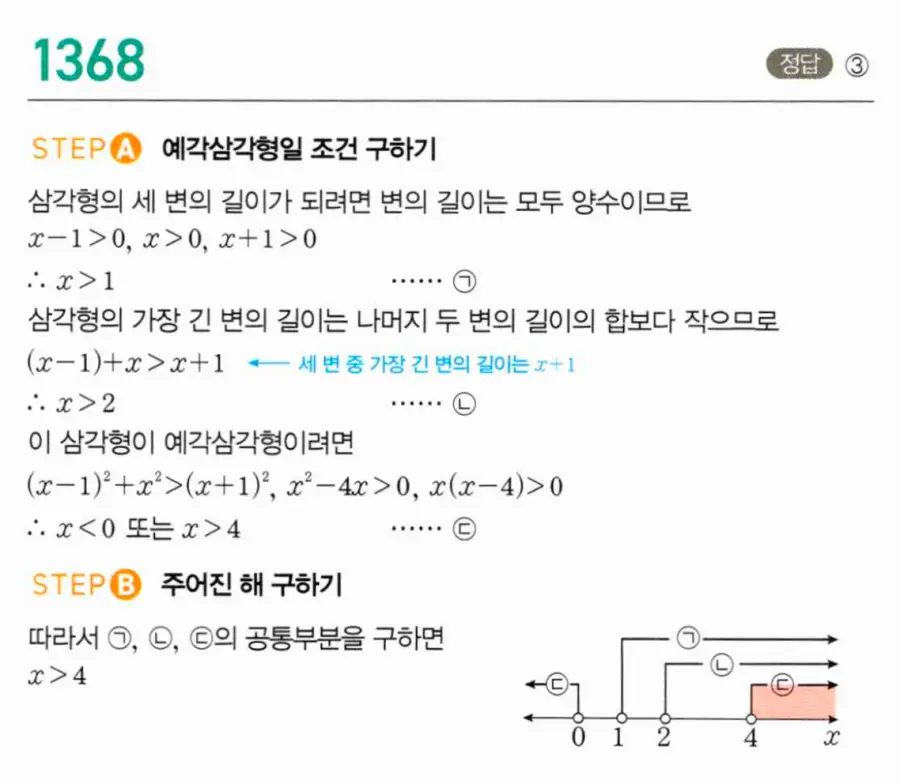
① 삼각형 성립 조건 — 변의 길이 양수 — x−1>0, x>0, x+1>0이므로 x>1 ……㉠.
② 삼각형 부등식 — 가장 긴 변 x+1 < 나머지 합: x+1<(x−1)+x이므로 x>2 ……㉡.
③ 예각삼각형 조건 — 세 변 중 가장 긴 변은 x+1. 예각삼각형이려면 (x+1)²<x²+(x−1)². 전개: x²+2x+1<x²+x²−2x+1, 즉 x²−4x>0이므로 x<0 또는 x>4 ……㉢.
④ x의 범위 결정 — ㉠, ㉡, ㉢의 공통부분: x>4.
정답: ③ x>4.
1368번 TOUGH 엄선 풀이영상
▲ 9단원 이차부등식 TOUGH · 예각삼각형 조건 (x+1)²
1368번 답지 확인