🔥 TOUGH
📋 2022년 03월 고2 학력평가 15번
마플시너지 공통수학1 1365번 TOUGH – 9단원 이차부등식, 연립부등식 {|x−k|≤5, x²−x−12>0} 모든 정수 x 값의 합 7이 되도록 하는 정수 k의 값
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 9단원 · 이차부등식 |
| 🔢 문제번호 | 1365번 |
| 📋 출처 | 2022년 03월 고2 학력평가 15번 |
| ⭐ 유형 | TOUGH |
마플시너지공수1답지 1365번 TOUGH 핵심 포인트
1365번은 9단원 이차부등식 TOUGH 문제(2022년 3월 고2 학평 15번)로, 연립부등식 {|x−k|≤5, x²−x−12>0}을 만족시키는 모든 정수 x의 값의 합이 7이 되도록 하는 정수 k의 값을 구하는 문제입니다.
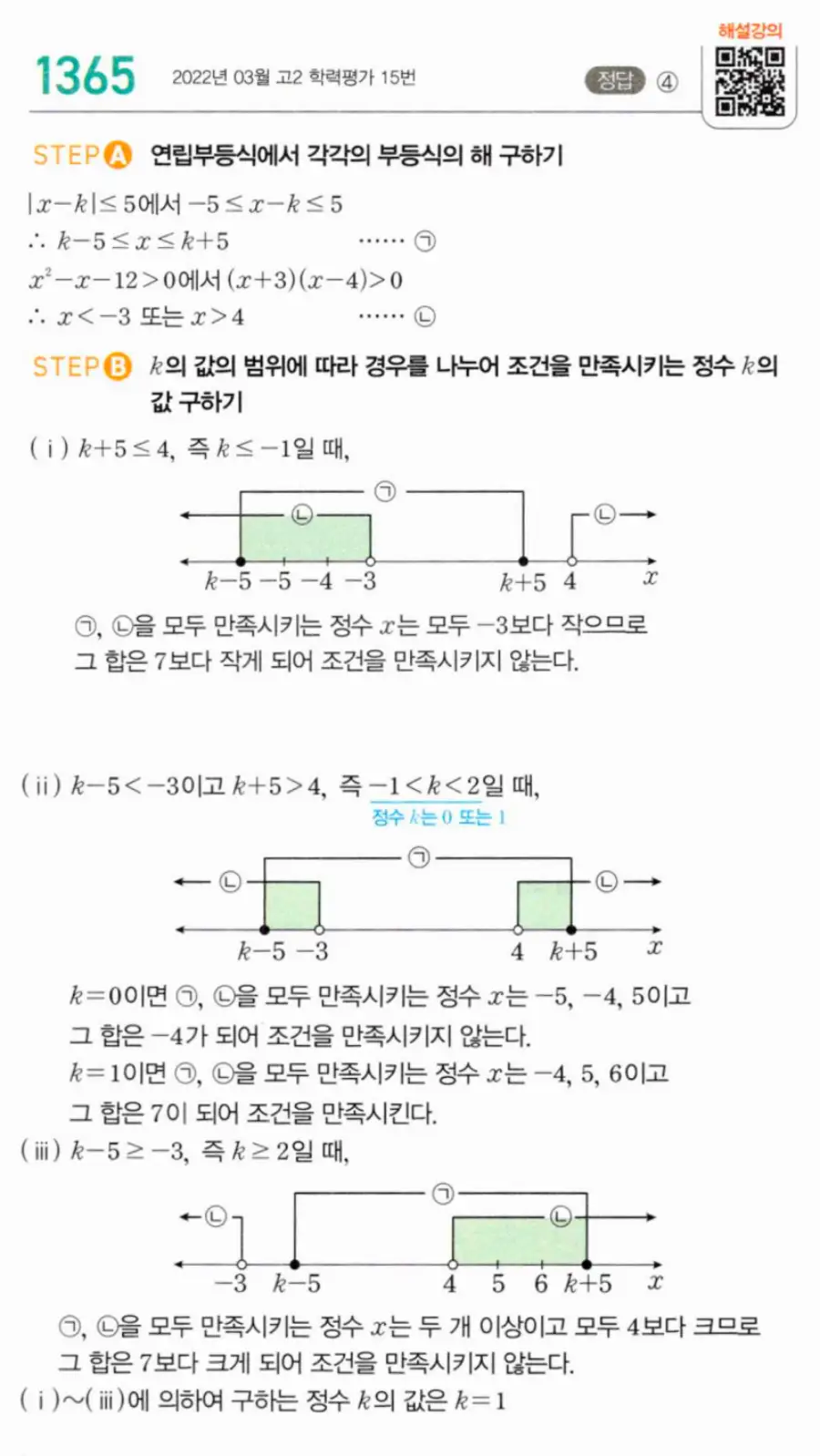
① |x−k|≤5 풀기 — −5≤x−k≤5이므로 k−5≤x≤k+5 ……㉠.
② x²−x−12>0 풀기 — (x+3)(x−4)>0이므로 x<−3 또는 x>4 ……㉡.
③ k의 범위에 따라 경우분류 — ㉠과 ㉡의 교집합에서 정수 x의 합이 7이 되도록 k값을 찾습니다.
④ k+5≤4, 즉 k≤−1일 때 — 정수 x는 모두 −3보다 작으므로 합이 7보다 작아 조건 불만족.
⑤ −1<k<2일 때 — k=0이면 합 −4, k=1이면 정수 x: −4, −5, 5, 6, 7, 8이고 합 확인. k=1일 때 ㉠: −4≤x≤6, ㉡과 교집합: −4와 5, 6. 정수 x: −4, 5, 6이고 합=7. 조건 만족.
⑥ k−5≥−3, 즉 k≥2일 때 — 정수 x는 모두 4보다 크므로 합이 7보다 커 조건 불만족.
따라서 정수 k의 값은 1.
정답: ④ 1.
1365번 TOUGH 엄선 풀이영상
▲ 9단원 이차부등식 TOUGH · |x−k|≤5와 x²−x−12>0 연립, 정수합 7 → k=1 · 1365번 전 과정 해설
1365번 답지 확인