🔥 TOUGH
마플시너지 공통수학1 1356번 TOUGH – 9단원 이차부등식, 연립부등식 {|x−2| ≤ a, x²+4x−(3a+2)(3a−2) > 0}의 해가 없을 때 양수 a의 최솟값
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 9단원 · 이차부등식 |
| 🔢 문제번호 | 1356번 |
| 📋 출처 | 자체 문항 |
| ⭐ 유형 | TOUGH |
마플시너지공수1답지 1356번 TOUGH 절댓값·이차부등식 연립 핵심 포인트
1356번은 9단원 이차부등식 TOUGH 문제로, 연립부등식 {|x−2| ≤ a, x²+4x−(3a+2)(3a−2) > 0}의 해가 없을 때 양수 a의 최솟값을 구하는 문제입니다.
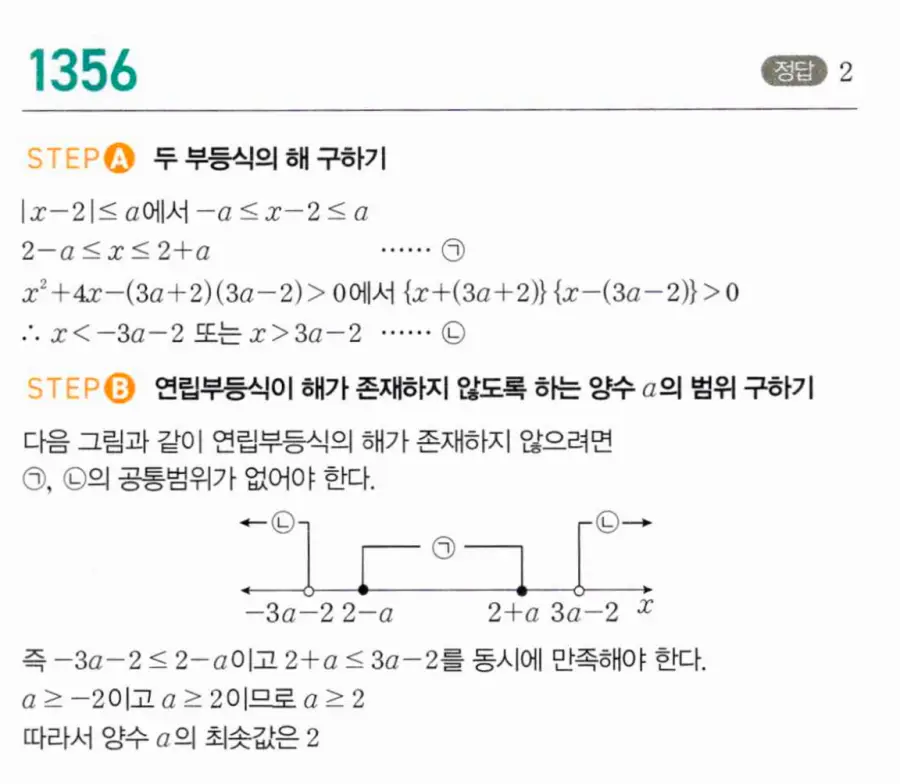
① STEP A. 두 부등식의 해 구하기 — |x−2| ≤ a에서 −a ≤ x−2 ≤ a이므로 2−a ≤ x ≤ 2+a ⋯ ⓐ. x²+4x−(3a+2)(3a−2) > 0에서 x²+4x−(9a²−4) > 0, {x+(3a+2)}{x−(3a−2)} > 0이므로 x < −3a−2 또는 x > 3a−2 ⋯ ⓑ.
② STEP B. 연립부등식이 해를 갖지 않도록 하는 양수 a의 범위 구하기 — ⓐ: 2−a ≤ x ≤ 2+a와 ⓑ: x < −3a−2 또는 x > 3a−2의 공통범위가 없으려면, ⓐ의 구간 [2−a, 2+a]가 ⓑ의 해 바깥에 있어야 합니다. 즉 −3a−2 ≤ 2−a이고 2+a ≤ 3a−2를 동시에 만족해야 합니다.
③ 조건 정리 — −3a−2 ≤ 2−a에서 −2a ≤ 4, a ≥ −2 (양수이므로 자동 성립). 2+a ≤ 3a−2에서 4 ≤ 2a, a ≥ 2.
따라서 양수 a의 최솟값은 2.
1356번 TOUGH 엄선 풀이영상
▲ 9단원 이차부등식 TOUGH · |x−2|≤a 구간이 ⓑ 해에 포함 안 됨 → a≥2 → 최솟값 2 1356번 전 과정 해설
1356번 답지 확인