🔥 TOUGH
📋 2024년 6월 고1 학평 27번
마플시너지 공통수학1 1351번 TOUGH – 9단원 이차부등식, 연립부등식 {x²−11x+24 < 0, x²−2kx+k²−9 > 0}의 해가 α < x < β, β−α = 2 → 모든 k의 합
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 9단원 · 이차부등식 |
| 🔢 문제번호 | 1351번 |
| 📋 출처 | 2024년 06월 고1 학력평가 27번 |
| ⭐ 유형 | TOUGH |
마플시너지공수1답지 1351번 TOUGH 연립이차부등식 핵심 포인트
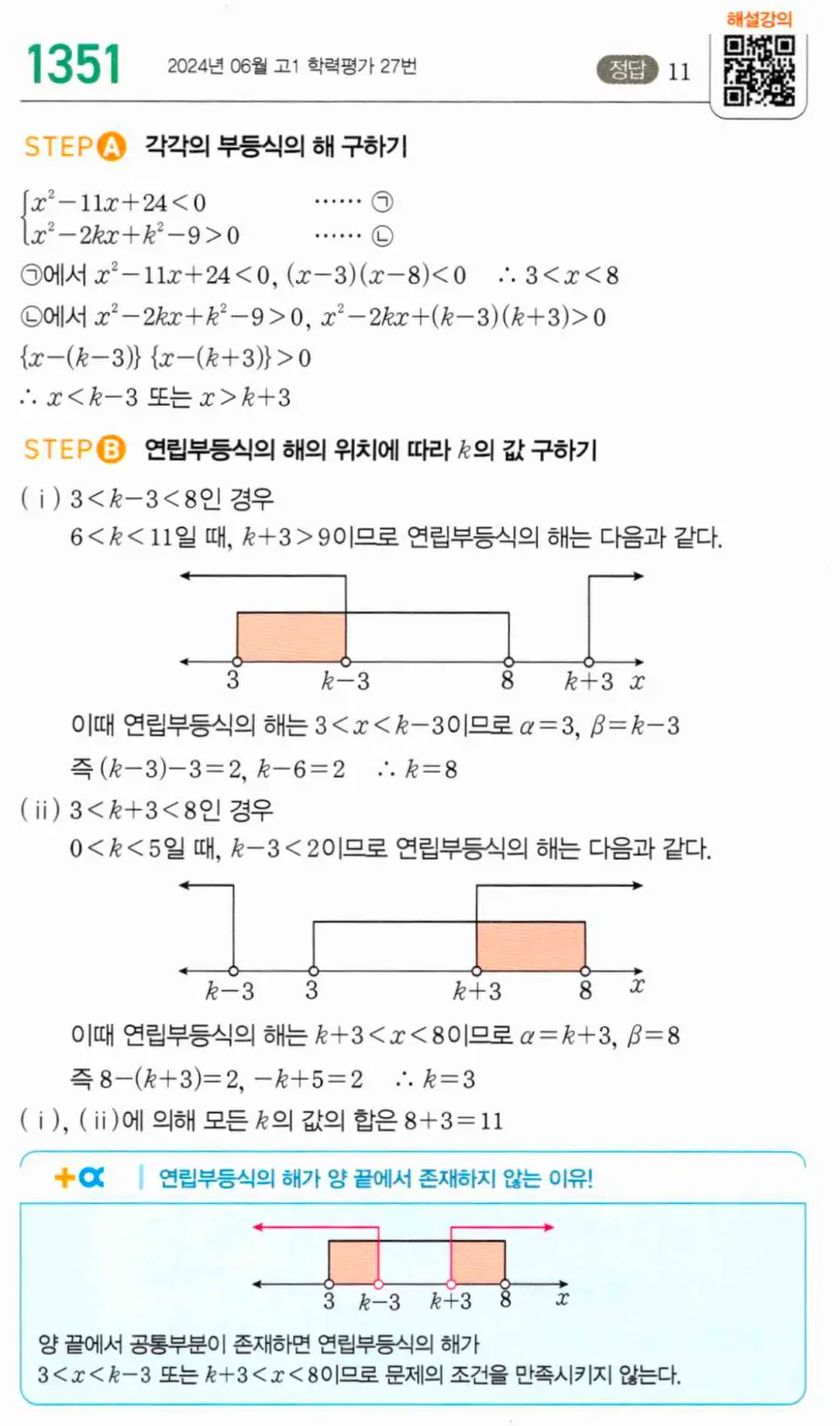
1351번은 9단원 이차부등식 TOUGH 문제(2024년 6월 고1 학평 27번)로, 연립부등식 {x²−11x+24 < 0, x²−2kx+k²−9 > 0}의 해가 α < x < β일 때, β−α = 2를 만족시키는 모든 실수 k의 값의 합을 구하는 문제입니다.
① STEP A. 각각의 부등식의 해 구하기 — x²−11x+24 < 0에서 (x−3)(x−8) < 0이므로 3 < x < 8 ⋯ ⓐ. x²−2kx+k²−9 > 0에서 x²−2kx+(k−3)(k+3) > 0, {x−(k−3)}{x−(k+3)} > 0이므로 x < k−3 또는 x > k+3 ⋯ ⓑ.
② STEP B. 연립부등식의 해의 위치에 따라 k의 값 구하기 — (ⅰ) 3 < k−3 < 8인 경우: 6 < k < 11일 때, k+3 > 9이므로 연립부등식의 해는 3 < x < k−3. β−α = (k−3)−3 = k−6 = 2에서 k = 8. (ⅱ) 3 < k+3 < 8인 경우: 0 < k < 5일 때, k−3 < 2이므로 연립부등식의 해는 k+3 < x < 8. β−α = 8−(k+3) = 5−k = 2에서 k = 3.
모든 k의 값의 합: 8+3 = 11.
1351번 TOUGH 엄선 풀이영상
▲ 9단원 이차부등식 TOUGH · 연립부등식 해 위치별 k 구하기 → k=8, k=3 → 합 11 1351번 전 과정 해설
1351번 답지 확인