📝 서술형 기출유형
마플시너지 공통수학1 1206번 서술형 기출유형 – 8단원 부등식, 연립부등식 { 2x+9 > 3x+2, 3x−a > x−3 }을 만족시키는 정수 x가 1개뿐일 때 실수 a의 값의 범위
| 📘 교재 | 마플시너지 공통수학1 |
| 📐 단원 | 8단원 · 부등식과 방정식 |
| 🔢 문제번호 | 1206번 |
| 📋 유형 | 연립부등식 · 정수 해 1개 조건 서술형 |
| ⭐ 난이도 | 서술형 기출유형 |
마플시너지공수1답지 1206번 서술형 정수 해 1개 조건 핵심 포인트
1206번은 8단원 부등식 서술형 기출유형으로, 연립부등식 { 2x+9 > 3x+2, 3x−a > x−3 }을 만족시키는 정수 x가 1개뿐일 때 실수 a의 값의 범위를 구하는 문제입니다.
[1단계] 부등식 2x+9 > 3x+2의 해를 구한다. [3점]
2x+9 > 3x+2에서 −x > −7, x < 7 ···㉮
[2단계] 부등식 3x−a > x−3의 해를 구한다. [3점]
3x−a > x−3에서 2x > a−3, x > (a−3)/2 ···㉯
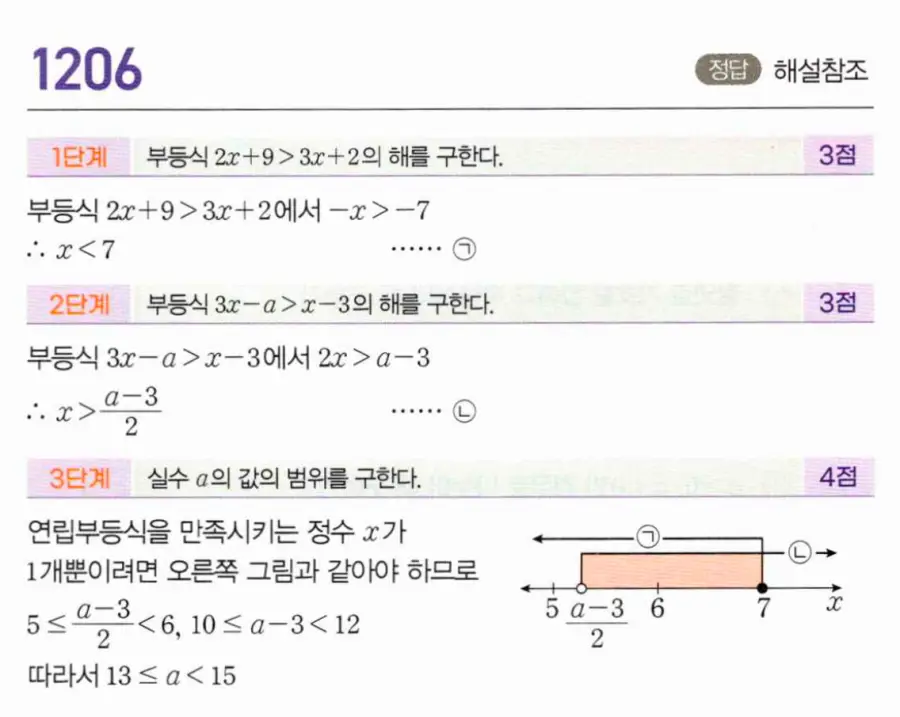
[3단계] 실수 a의 값의 범위를 구한다. [4점]
연립부등식의 해는 (a−3)/2 < x < 7. 이 범위에 정수 x가 1개뿐이려면 그 정수는 x = 6이어야 합니다. 수직선에서 정수 6만 포함되려면 5 ≤ (a−3)/2 < 6. 양변에 2를 곱하면 10 ≤ a−3 < 12, 따라서 13 ≤ a < 15.
1206번 서술형 기출유형 엄선 풀이영상
▲ 8단원 부등식 서술형 · (a−3)/2 < x < 7에서 정수 x=6만 → 13≤a<15 1206번 전 과정 해설
1206번 답지 확인